원고
와커 헤미 아게(Wacker Chemie AG) (소송대리인 변리사 신윤숙 외 1인)
피고
오씨아이 주식회사(OCI Company Ltd.) (소송대리인 법무법인(유한) 광장 담당변호사 조용진 외 2인)
2019. 12. 5.
주문
1. 원고의 청구를 기각한다.
2. 소송비용은 원고가 부담한다.
특허심판원이 2018. 10. 10. 2017당2655 사건에 관하여 한 심결 을 취소한다.
이유
1. 기초사실
가. 원고의 이 사건 특허발명(갑 제3호증)
1) 발명의 명칭: 다결정 실리콘의 제조 방법
2) 우선일/ 출원일/ 등록일/ 등록번호: 2010. 9. 1./ 2011. 8. 25./ 2014. 1. 22. / (특허등록번호 생략)
3) 특허청구범위
【청구항 1】 다결정 실리콘의 제조 방법으로서(이하 ‘구성요소 1’이라 한다), 상기 방법은, 실리콘-함유 성분 및 수소를 포함하는 반응 개스를 하나 이상의 노즐에 의해 반응기에 도입하는 단계를 포함하며(이하 ‘구성요소 2’라 한다), 상기 반응기는 실리콘이 증착되는 하나 이상의 가열되는 필라멘트 봉을 포함하며(이하 ‘구성요소 3’이라 한다), 반응기의 공부피(empty volume)에 대한 봉의 부피의 비(백분율)를 의미하는 충전 수준(fill level: FL)의 함수로서 반응기내 유동조건(flow condition)을 나타내는 아르키메데스 수(Archimedes number: Arn)가(이하 ‘구성요소 4’라 한다), 충전 수준 FL이 5% 이하인 경우에는 함수 Ar = 2000 x 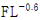 에 의한 하한값과 함수 Ar = 17000 x
에 의한 하한값과 함수 Ar = 17000 x 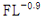 에 의한 상한값으로 정해지는 범위 내이며, 충전 수준 FL이 5% 보다 큰 경우에는 750 내지 4000인(이하 ‘구성요소 5’라 한다), 다결정 실리콘의 제조 방법(이하 ‘이 사건 제1항 발명’이라 하고 나머지 청구항에 대해서도 같은 방식으로 부른다).
에 의한 상한값으로 정해지는 범위 내이며, 충전 수준 FL이 5% 보다 큰 경우에는 750 내지 4000인(이하 ‘구성요소 5’라 한다), 다결정 실리콘의 제조 방법(이하 ‘이 사건 제1항 발명’이라 하고 나머지 청구항에 대해서도 같은 방식으로 부른다).
【청구항 2】제1항에 있어서, 상기 아르키메데스 수가 충전 수준 4.5-5.5% 범위에서 선택되는 임의의 지점까지는 감소하고, 상기 선택되는 지점보다 높은 충전 수준에서는 일정하게 유지되는 것을 특징으로 하는 다결정 실리콘의 제조 방법.
【청구항 3】제1항에 있어서, 상기 아르키메데스 수가 충전 수준 6.5-7.5% 범위에서 선택되는 임의의 지점까지는 감소한 다음 일정하게 유지되고, 상기 아르키메데스 수의 감소구간 중 4.5%보다 높은 충전 수준에서는 상기 아르키메데스 수가 1-3%의 충전 수준의 경우보다 더 급격하게 감소하는 것을 특징으로 하는 다결정 실리콘의 제조 방법.
【청구항 4】제1항에 있어서, 상기 아르키메데스 수가 충전 수준 4.5-5.5% 범위에서 선택되는 임의의 지점까지는 감소하고, 상기 선택되는 지점보다 높은 충전 수준에서는 증가하는 것을 특징으로 하는 다결정 실리콘의 제조 방법.
【청구항 5】제1항 내지 4항 중 어느 한 항에 있어서, 상기 반응기의 체적은 300K 내지 700K의 온도를 가진 벽에 의해 한정되는 것을 특징으로 하는 다결정 실리콘의 제조 방법.
【청구항 6】제1항 내지 4항 중 어느 한 항에 있어서, 상기 반응기의 외벽에 상기 벽과 대면하는 하나 이상의 봉의 일측과 상기 하나 이상의 봉의 높이의 중간 지점에서 측정되는 봉의 온도가 1150K 내지 1600K인 것을 특징으로 하는 다결정 실리콘의 제조 방법.
【청구항 7】제1항 내지 4항 중 어느 한 항에 있어서, 실리콘 증착 후 적어도 하나 이상의 봉이 상기 반응기로부터 제거된 다음 기계적으로 가공되어 실리콘 청크(silicon chunk)를 형성하는 것을 특징으로 하는 다결정 실리콘의 제조 방법.
【청구항 8】제1항 내지 4항 중 어느 한 항에 있어서, 상기 방법에 의해 제조되는 다결정 실리콘은 대역 용융법(zone melting), 초크랄스키 방법(Czochralski process), 또는 블록 주조법(block casting)에 의한 단결정 실리콘의 제조용으로 사용되는 것을 특징으로 하는 다결정 실리콘의 제조 방법.
4) 발명의 주요 내용
| [1] 기술분야 |
| 【0001】 본 발명은 다결정 실리콘의 제조 방법에 관한 것이다. |
| [2] 배경기술 |
| 【0002】 다결정 실리콘(간단히 폴리실리콘이라 함)은 도가니 인상방법(Czochralski 또는 CZ 공정) 또는 대역 용융 공정(zone melting process)에 의한 단결정 실리콘의 제조 공정에서 출발 물질로서 작용한다. 단결정 실리콘은 웨이퍼로 분리되고, 여러 가지 기계적, 화학적 및 화학기계적 처리 공정을 거친 후, 전자 부품(칩)의 제조를 위해반도체 산업에서 사용된다. |
| 【0003】 그러나, 보다 상세하게는, 다결정 실리콘은 인상 또는 주조 공정에 의한 단결정 또는 다결정 실리콘의 제조를 위해 다량으로 필요하며, 이러한 단결정 또는 다결정 실리콘은 광전 소자용의 태양 전지의 제조를 위해 사용된다. |
| 【0004】 다결정 실리콘은 전형적으로는 지멘스 공정(Siemens process)에 의해 제조된다. 이 공정에서, 얇은 필라멘트 봉(얇은 봉)은 벨- 형 반응기(지멘스 반응기)에 전류를 직접 통과시킴으로써 가열되며, 실리콘- 함유 성분 및 수소를 포함하는 반응 개스가 주입된다. |
| 【0005】 반응 개스 중의 실리콘-함유 성분은 일반적으로 일반식 SiHnX₄-n (n = 0, 1, 2, 3; X = Cl, Br, I)의 모노실란 또는 할로실란이다. 바람직하기로는, 클로로실란, 클로로실란 혼합물, 더욱 바람직하기로는 트리클로로실란이다. 주로 SiH₄ 또는 SiHCl3가 수소와의 혼합물로 사용된다. |
| 【0006】 EP 2077252 A2 는 폴리실리콘의 제조에 사용되는 반응기의 전형적인 구조에 대해 개시하고 있다. |
| 【0007】 반응기 베이스는 전극을 구비하고 있으며, 이 전극에는 얇은 봉이 수납되어 있고, 성장 공정 동안에 실리콘이 얇은 봉에 증착됨에 따라 폴리실리콘으로 만들어진 원하는 봉으로 성장하게 된다. 일반적으로, 각각의 경우에, 두 개의 얇은 봉이 브릿지에 의해 연결되어 한쌍의 얇은 봉이 만들어지고, 이것이 전극과 외부 소자를 통해 회로를 형성하게 되고, 쌍을 이룬 봉들을 특정 온도로 가열하는 작용을 한다. |
| 【0008】 봉의 온도는 일반적으로 수직 봉의 표면에서 방사선 고온계(radiation pyrometer)에 의해 측정된다. |
| 【0009】 봉의 온도는 일반적으로 전력을 고정방식으로 또는 봉의 직경의 함수로서 제어함으로써 설정된다. |
| 【0010】 또한, 반응기 베이스는 추가로 반응기에 신선한 개스를 공급하는 노즐을 구비한다. 방출 개스는 구멍을 통해 반응기 챔버로부터 이송된다. |
| 【0011】 공급되는 반응 개스의 양은 일반적으로 봉의 직경의 함수로서 달라지는데, 즉 일반적으로 봉의 직경이 커지면 공급되는 반응 개스의 양도 증가된다. |
| 【0012】 가열된 봉과 브릿지에 고순도 폴리실리콘이 증착되고, 시간이 경과함에 따라 봉의 직경이 성장한다(CVD = Chemical vapor deposition/gas phase deposition). |
| 【0013】 증착 공정이 종료된 후, 생성된 폴리실리콘 봉은, FZ(Float Zone) 공정에 의한 단결정 제조용으로 사용되지 않는 한, 럼프(lumps) 및 칩으로 가공되어야 한다. |
| 【0014】 후자의 경우에, 폴리실리콘 봉이 대역 용융법에 의해 단결정 실리콘 잉곳을 제조하는데 사용되며, 단결정 실리콘 잉곳은 후속 단계에서 추가로 가공되어 실리콘 웨이퍼로 만들어진다. |
| 【0015】 CZ 공정 또는 태양 전지용 실리콘 청크(chunk)를 제조하기 위해, 봉은 기계적으로 해머, 분쇄기 또는 밀(mill)과 같은 공구에 의해 분쇄된 다음 크기별로 분류된다. 실리콘 조각의 크기는 약 1 mm 내지 150 mm 또는 그 이상까지 다양하다. 실리콘 조각의 형태는 일반적으로 구형에서 크게 벗어나지는 않는다. |
| 【0016】 지멘스 공정을 토대로 하는 폴리실리콘 증착 공정으로서 공지된 모든 방법들은 달성되는 생성물의 품질이 좋지 않으며, 제조 공정의 경제성이 떨어진다. |
| 【0017】 생성물의 품질에 관한 단점은 특히 봉의 직경에 있어서 축방향으로 변동이 관찰되는 경우가 흔하며, 어떤 경우에는 봉의 표면 특성이 불량하다. |
| 【0018】 상기 공정들은 상승된 수준의 에너지를 필요로 하는 경우가 흔하다. |
| 【0019~0021】 어떤 경우에는 봉이 반응기 안에서 넘어지고, 일부 공정에서는 실리콘 분진이 형성되거나, 과열이 일어나고, 최악의 경우 실리콘 캐리어 본체(봉 및 브릿지)의 용융도 발생된다. |
| 【0023】 EP 2 077 252 A2에서는, 공정 기술의 관점에서, 증착 공정 동안에 반응 개스 공급을 위한 노즐을 ON/OFF 스윗칭 하는 것이 유리한 것으로 기재되어 있다. 이를 위해, 닫힌 노즐의 비율을 공정 시간 또는 봉의 직경의 함수로서 조절한다. |
| 【0024】 이러한 방법의 목적은, 봉의 직경이 성장함에 따라, 모든 봉의 최적 개스 공급을 특히 더 높은 수준의 범위 내로 보장하기 위한 것이다. |
| 【0025】 EP 2 067 744 A2는 다결정 실리콘의 제조 방법을 개시하고 있는데, 이 방법에서는 첫 번째 안정화 단계 후 실리콘 증착을 위한 반응 개스의 유입 속도를 처음에는 크게 증가시키고, 그 다음에는 얇은 봉에 대한 반응 개스의 공급을 증가시키기 위해 좀 더 늦추고, 성장 단계에서는 효율적인 증착을 위해 저감시킨다. 반응 개스의 공급만을 조절함으로써, 반응기에 대한 변형은 전혀 필요하지 않다는 것을 강조하고 있다. |
| 【0026】 그러나, EP 2 077 252 A2 및 EP 2 067 744 A2에 개시된 공정들에 의하면 반응기에서 넘어지는 봉의 수가 증가되는 것으로 나타났다. 이는 아마도 반응 개스의 유입 속도의 갑작스러운 변화와 관련이 있는 것으로 보인다. |
| 【0027】 사용되는 얇은 봉의 길이는 수 미터(통상 2-3 m)일 수 있다. 봉이 넘어지는 경우, 인접하는 다른 봉을 건드릴 수도 있다. |
| 【0028】 이는 상당한 경제적인 손실을 야기하며, 이런 식으로 오염된 실리콘 봉을 복잡한 방식으로 세정해야 하는 경우에 특히 그러하고, 봉이 넘어질 때 반응기가 손상되는 경우에는 더욱 그러하다. |
| 【0029】 증착 공정이 완료되기 전에 이러한 경우가 발생하면, 넘어진 봉을 복구하기 위해 증착 공정을 즉시 중단시켜야 한다. 이는 해당 플랜트의 경제성에 직접적인 영향을 미친다. 반응기에 봉이 많이 있을수록 경제적인 손실은 커진다. 한편, 정상적인 작동시에 높은 경제성은 반응기 내 많은 수의 봉과 직접 연관된다. |
| 【0030】 EP 2 067 744 A2에 개시된 공정의 또 다른 단점은, 봉의 전장에 걸쳐 일정한 구조 또는 형태를 달성하는 것과 동시에 충분히 높은 증착 속도를 달성하는 것이 확실히 불가능하다는 것이다. |
| 【0031】 증착 공정 동안 실리콘 봉의 구조는 이상적으로는 커지는 반경의 실린더에 대응한다. 이러한 실린더 형태에서 일탈하면 공정에 혼란이 야기될 수 있다. 가장 좋지 않은 경우에는, 봉들이 함께 융합될 수 있고 증착 공정이 중단될 수 있다. 상기 언급한 일탈의 예를 들면, 형태가 하방으로 좁아지는 원추형인 경우에는 중량의 분포가 불리하게 됨에 따라 봉이 넘어지게 될 위험성이 증가한다. |
| 【0032】 후에 FZ 공정에 사용될 폴리실리콘에 대한 요건이 특히 엄격하다. 사용 전에, 봉을 공칭 직경을 가진 구형으로 분쇄(grinding)해야 한다. 타겟 직경을 조금이라도 초과한다는 것은, 구형 분쇄 과정에서 제거되는 물질의 양이 증가된다는 것이며, 따라서 귀중한 실리콘이 손실된다는 것을 의미한다. 반면, 직경이 타겟 직경보다 작으면, 사용되는 봉의 길이가 감소되므로, 타겟 생성물의 경제성이 악화된다는 것을 의미한다. |
| 【0033】 폴리실리콘 봉은 길이 및 직경 뿐만 아니라 추가적인 파라미터에 의해서도 설명될 수 있다: 봉의 표면의 성질은 다를 수 있다. 봉은 콜리플라워와 같은 표면을 가질 수 있다. 그러나 봉은 또한 거의 평탄한 표면을 가질 수도 있다. 봉의 표면의 전체적인 성질은 이하 "형태(morphology)"라는 용어로 언급될 것이다. |
| 【0034】 기본적으로 높은 평균증착속도(mean deposition rate)는 높은 생산성을 얻기 위해서는 필수적으로 중요하며, 따라서 공정의 경제성을 얻기 위해서도 중요하다. 그러므로, 증착속도를 가능한 한 최대화시키기 위한 노력이 경주되어 왔다. 그러나, 높은 증착속도는 통상적으로 예를 들어 형태에 악영향을 미치는 공정 조건을 필요로 한다. |
| 【0035】 DE 102 007 047 210 A1은 유리한 굽힘 강도(flexural strength)를 가진 폴리실리콘 봉을 만드는 방법을 개시하고 있다. 또한, 이 공정에서 비에너지 소비는 특히 낮다. 공정 기술 관점에서, 클로로실란 혼합물의 유속의 최대값은 30 시간 이내, 바람직하기로는 5시간 이내에 달성되며, 브릿지의 하면의 온도는 1300℃ 내지 1413℃이다. |
| 【0036】 문제는 브릿지의 내부의 온도가 DE 102 007 047 210 A1에 따른 1300℃ 내지 1413℃로 유지되는 브릿지 표면의 온도보다 높을 수 있다는 것이다. |
| 【0037】 온도는 봉과 브릿지에서 전류에 의해 조절된다. 개스 유입에 의한 브릿지 표면의 냉각의 경우에 온도가 유지될 수 있도록 하기 위해서는, 전류가 증가되어야 한다. |
| 【0038】 실리콘과 같은 반도체들은 온도가 높아질수록 전기 저항이 저하되는 성질을 가지고 있는 것으로 알려져 있다. |
| 【0039】 가열된 봉의 내부의 온도가 반응 개스에 의해 냉각되는 그 표면의 온도보다 높기 때문에 봉의 내부와 브릿지의 전기 저항이 낮아진다. 그러므로, 브릿지 내부의 전류는 높아진다. 반응 개스에 의한 브릿지 표면의 극심한 냉각으로 인해 열 유동이 높아지는 제한된 경우에, 브릿지 내부의 온도가 실리콘의 융점(1413℃)보다 높아질 수 있다. 이로 인해 브릿지 누출(bridge leakage)을 초래할 수 있으며, 이는 불가피하게 증착 공정의 중단을 초래한다. |
| 【0040】 DE 10 2007 047 210 A1은 브릿지 누출의 가능성이 크게 증가되는 공정을 개시하고 있다. |
| 【0041】 이것은 브릿지 온도를 저하시키는 것에 의해서만 방지될 수 있지만, 이는 다시 비교적 높은 증착 속도와 개선된 에너지 효율이라는 장점을 무력화시키게 될 것이다. |
| 【0042】 DE 10 2007 023 041 A1은 폴리실리콘, 특히 FZ 실리콘의 제조를 위한 또 다른 방법을 개시하고 있다. 그 방법에 따르면, 봉의 직경이 30 mm가 될 때 까지는, 950 내지 1090℃의 봉 온도, 반응 개스 중의 클로로실란 비율을 특정 값으로 유지하고, 늦어도 봉 직경이 120 mm에 도달한 후에는, 봉의 온도를 930 내지 1030℃로 전환하고 반응 개스 중의 클로로실란의 비율을 증가시킨다. 증착 기간 전체에 걸쳐 성장 조건의 급격한 변화는 없어야 한다. |
| 【0043】 FZ 실리콘의 제조를 위해 사용되는 폴리실리콘 봉은 증착 후 전형적으로는 기계적인 가공 수단에 의해 원하는 직경으로 만들어진다. 실리콘의 손실을 최소화시키기 위해, 생성되는 모든 봉이 전체 길이에 걸쳐 동일한 직경을 가져야 한다. 또한, 봉의 단면은 전체 길이에 걸쳐 원형이어야 한다. |
| 【0044】 그러나, DE 10 2007 023 041 A1에 따라 제조되는 폴리실리콘 봉은 결정의 길의의 함수로서 직경이 충분히 일정하지는 않은 구조를 나타낸다. 직경은 결정의 길이에 따라 다르며, 이는 기계적인 가공 후 공칭 직경을 얻기 위해서는 한쪽의 물질이 더 많이 제거되어야 하는 결과를 초래한다. 이는 공정의 경제성을 떨어뜨린다. |
| 【0045】 실리콘- 함유 개스가 봉의 표면에 증착되지 않고 (불균일 증착), 그 대신 반응하여 자유 부피의 실리콘을 생성 (균일 증착)하는 경우를 분진 증착(dust deposition)이라고 한다. |
| 【0046】 형성된 분진은 먼저 증착 공정의 종료 시점에서 반응기의 베이스에서 발견되는데, 후속 단계에서 처분되어야 한다. |
| 【0047】 두 번째로, 분진은 방출 개스와 함께 방출 개스 처리부로 이송되어, 문제를 야기할 수 있다. |
| 【0048】 심각한 분진 증착은 증착 공정을 중단시킬 수 있고, 이는 경제성을 떨어뜨린다. |
| 【0049】 또한, 그것은 공업 시설에 상당한 문제를 야기하며, 이와 관련하여 추가의 비용과 불편을 초래한다. |
| 【0050】 불행하게도, 특히 높은 증착 속도를 이용하는 특별한 증착 공정은 일부 경우에 분진 증착을 증가하는 것으로 밝혀지고 있다. |
| 【0051】 결론적으로, 지금까지의 종래 기술로는 폴리실리콘의 증착 공정에서 중요한 여러 가지 측면을 조화시키는 것이 불가능했다. |
| [3] 과제의 해결 수단 |
| 【0053】 본 발명의 전술한 목적은 본 발명의 다결정 실리콘의 제조 방법에 의해 달성되는데, 상기 방법은, 실리콘- 함유 성분 및 수소를 포함하는 반응 개스를 하나 이상의 노즐에 의해 반응기에 도입하는 단계를 포함하며, 상기 반응기는 실리콘이 증착되는 하나 이상의 가열되는 필라멘트 봉을 포함하며, 반응기의 공부피(empty volume)에 대한 봉의 부피의 비(백분율)를 의미하는 충전 수준(fill level: FL)의 함수로서 반응기내 유동 조건을 나타내는 아르키메데스 수(Archimedes number: Arn)가 5%까지의 충전 수준 FL에 대해서는 함수 Ar = 2000 x FL-0.6에 의한 하한값과 함수 Ar = 17000 x FL-0.9에 의한 상한값으로 정해지는 범위 내이며, 충전 수준 FL이 5% 보다 큰 경우에는 750 내지 4000인 것을 특징으로 한다. |
| 【0054】 공정의 성공을 위해서는, 강제 대류(forced convection)에 대한 자유 대류(free convection)의 비로서 반응기 내 유동 조건을 의미하는 아르키메데스 수가 정해진 범위 내에 존재하도록 공정을 수행하는 것이 필수적이다. 이 범위는 전체 공정 기간에 대해 정해진다. |
| 【0055】 이러한 목적을 위해, 아르키메데스 수는 반응기의 충전 수준의 함수로서 보고되어 있다. |
| 【0056】 반응기의 충전 수준은 반응기의 공부피에 대한 봉의 부피의 비(백분율)를 의미한다. 반응기의 공부피는 일정하다. |
| 【0057】 그러므로 공정 기간이 증가하면 봉의 부피가 증가하기 때문에 충전 수준이 증가한다. |
| 【0058】 상기 공정과 아르키메데스 수에 대한 본 발명의 범위는 반응기의 크기와 관계 없다. 그러므로 상기 공정은 작은 반응기와 큰 반응기 모두에 대해 적절하게 적용된다. |
| 【0059】 마찬가지로, 상기 공정은 반응기에 존재하는, 실리콘이 증착되는 필라멘트 봉의 수 및 길이와는 관계 없다. |
| 【0060】 아르키메데스 수에 의한 용기 내 유동 조건에 대한 일반적인 설명은 엔지니어링 열역학 텍스트북(예: Dittmann/Fischer/Huhn/Klinger, "Repetitorium der technischen Thermodynamik" [Refresher in Engineering Thermodynamics], Teubner Verlag (1995))에 공지되어 있다. |
| 【0061】 아르키메데스 수는 또한 "리차드슨 수(Richardson number)로도 알려져 있다. |
| 【0062】 다결정 실리콘의 증착을 위한 지멘스 반응기에 대해서는 아르키메데스 수와 관련하여 아직 아무런 평가가 이루어져 있지 않다. |
| 【0063】 실리콘의 증착에 사용되는 지멘스 반응기는 소정의 부피(공부피)를 가진 용기로서 간주될 수 있는데, 상기 부피는 특정 온도 Twall를 가진 벽에 의해 한정된다. 또한, 이 공간은 실리콘의 증착 결과 시간이 경과함에 따라 성장하며 특정 온도 Trod를 가진 봉을 수납한다. |
| 【0064】 개스는 가열된 봉에서 가열되어 상방으로 올라간다. 벽에서 개스가 다시 냉각되고 하방으로 내려온다. 이 과정을 개스의 자유 대류라고 한다. |
| 【0065】 또한, 반응 개스(수소 및 실리콘을 함유하는 개스로서, 예를 들어 트리클로로실란과 디클로로실란의 혼합물)는 일반적으로 베이스에 장착된 노즐에 의해 정해진 유입 속도로 이 공간으로 능동적으로 유입된다. 이것이 강제 대류를 야기한다. |
| 【0066】 동시에 방출 개스가 용기로부터 방출되고 용기 내 압력이 전형적으로는 일정하게 유지된다. |
| 【0067】 자유 대류는 부력에 기인하고, 강제 대류는 관성력에 기인한다. 이러한 2개의 유동력의 상호 작용이 외관상으로는 복잡한 유동 조건과 반응기 내 증착에 대한 그 효과를 지배하는 것으로 나타났다. 그러므로, 관성력에 대한 부력의 비로서 정의되는 아르키메데스 수가 유동 조건을 특성화하는 데 적합하다. |
| 【0068】 지멘스 반응기에서 봉에 대한 아르키메데스 수의 구체적인 유도 방법에 대해서는 여기서는 다시 설명하지 않기로 한다. |
| 【0069】 그 결과는 다음 관계식으로 표시된다: |
| 【0070】 Ar = Π * g * L³ * Ad * (Trod - Twall) / (2 * Q² * (Trod + Twall)) |
| 【0071】 상기 식에서, g는 중력으로 인한 가속도이고 그 단위는 m/s²이며, L은 필라멘트 봉의 길이이고 그 단위는 m이며, Q는 작동 조건(p, T) 하에서 개스의 체적 유량(volume flow)이며, 그 단위는 m³/s이고, Ad는 모든 노즐의 단면적의 합이며, 그 단위는 ㎡이고, Trod는 봉의 온도이고 그 단위는 K이며, Twall은 벽의 온도이고 그 단위는 K이다. |
| 【0072】 필라멘트 봉의 길이는 증착 기간 동안에, 예를 들어 L = 3m와 같이 반드시 일정하게 유지된다. |
| 【0073】 반응기가 반응 개스의 주입을 위해 동일 또는 상이한 단면을 가진 하나 이상의 노즐을 포함하는 경우, 모든 노즐의 단면적의 합 Ad(단위: ㎡)을 고려한다. 하나 또는 그 이상의 노즐의 단면적은 시간이 경과함에 따라 달라질 수도 있다. |
| 【0074】 모든 단면적의 합 Ad는 바람직하기로는 5 x 10-5㎡ 내지 약 1x 10-²㎡ 이다. |
| 【0075】 봉의 온도는 바람직하기로는 1150 K 내지 1600 K 이다. |
| 【0076】 벽의 온도는 바람직하기로는 300 K 내지 700 K 이다. |
| 【0077】 체적 유량은 바람직하기로는 작동 조건하에서 0.001m³/s 내지 0.5m³/s 이다. |
| 【0078】 하나의 반응기에 여러 개의 필라멘트 봉이 들어 있는 경우에는, 아르키메데스 수는 이들 봉의 수 n에 대한 합으로서 결정된다. 그 결과는 Arn 이다. |
| 【0079】 그 식은 다음과 같다: |
| 【0080】 Arn = n * Ar |
| 【0081】 그러나, 본 발명에 따른 공정은 이미 앞서 언급한 바와 같이 반응기 내의 봉의 수와 관계가 없다. |
| 【0082】 본 발명자들은, 반응기 내 봉의 수를 두 배로 할 때 반응 개스의 체적 유량을 단순히 두 배로 한다고 해도 성공적인 결과가 얻어지지 않는다는 것을 알게 되었는데, 그 이유는 그러한 공정이 충전 수준에 대한 아르키메데스수의 의존성을 보여주고 있기 때문인데, 그 수는 본 발명의 경우의 범위보다 낮다. 상기 공정은 또한 증가된 비에너지 소비와 넘어지는 봉의 비율이 증가되는 것을 보여준다. 반면, 예를 들어, 노즐 구조가 조절되면, 넘어지는 봉의 비율이 낮아지고 비에너지 소비가 낮아질 수 있다. 봉의 수를 두 배로 증가시키는 경우에 최적 공정은 다시 본 발명에 따른 공정에서 청구된 유동 조건에 대응하는 유동 조건을 필요로 한다. |
| 【0083】 아르키메데스 수가, 5%까지의 충전 수준 FL에 대해서는 함수 Ar = 2000 x FL-0.6 에 의한 하한값과 함수 Ar = 17000 x FL-0.9에 의한 상한값으로 정해지는 범위 내이고, 충전 수준 FL이 5% 보다 큰 경우에는 750 내지 4000의 범위 내인 모든 공정의 경우에, 다음과 같은 유리한 기술적인 효과가 동시적으로 및 반복적으로 발생한다. |
| 【0084】 종래 기술과 동일하거나 또는 종래 기술보다 높은 평균 증착 속도에서는 분진 증착이 거의 관찰되지 않는다. |
| 【0085】 본 발명에 따른 공정이 수행될 때, 봉 및/또는 브릿지의 누출이 발생하지 않는다. |
| 【0086】 본 발명의 명세서에 있어서, 봉의 온도는 수직 봉의 표면, 바람직하기로는 반응기의 외벽에 가장 가까운 봉의 측면에서, 봉의 높이의 중간 지점에서 방사선 고온계에 의해 측정된다. 따라서, 표면 온도는 봉의 중간 지점에서 조절된다. 그러므로, 전체 반응기에 대한 최적 유동 조건과 관련하여, 브릿지의 누출이 방지된다. |
| [4] 발명의 효과 |
| 【0087】 본 발명의 방법에 따르면, 넘어지는 봉의 비율은 종래 기술에서 알려진 공정의 경우에 비해 훨씬 낮은 것으로 나타났다. |
| 【0088】 본 발명의 방법에 의해 제조되는 모든 다결정 봉은 종래 기술과 바교하여 봉의 길이에 걸쳐 직경의 편차가 작다. |
| 【0089】 또한, 본 발명에 따른 방법에 있어서, 실리콘 봉의 형태는 봉 상의 축 위치와 무관하고, 증착 설비 내 봉의 위치와도 무관하며, 즉 위치에 관계 없이 모든 봉이 유리한 형태를 가지고 있는 것으로 나타났다. |
| [5] 발명의 실시를 위한 구체적인 내용 |
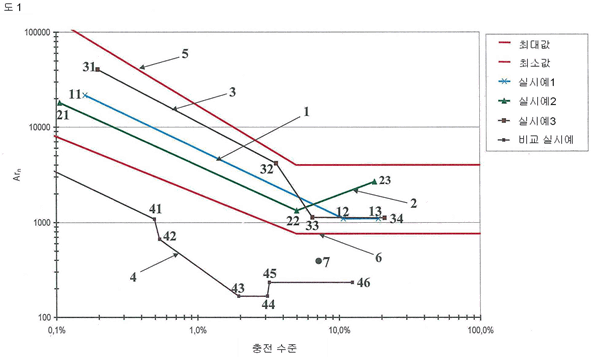
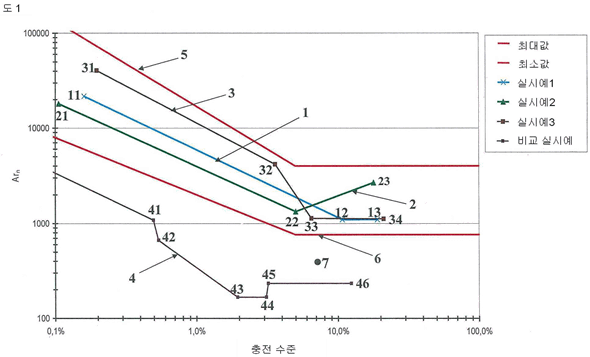
| 【0092】 도 1은 충전 수준의 함수로서 아르키메데스 수의 바람직한 범위를 나타낸다. 곡선이 이중- 로그 형태(double-logarithmic form)로 나타나 있다. |
| 【0093】 본 발명의 범위는 아르키메데스 수의 최대 및 최소 프로파일을 보여주는 라인 5와 6으로 나타나 있다. FL = 5% 까지는, 이들 라인은 지수 함수를 나타낸다. |
| 【0094】 FL = 5% 이하에서는, 두 개의 곡선 5와 6의 기울기는 이중- 로그 그래프에서 서로 상이하다. 따라서, 두 개의 지수 함수는 상이한 지수를 가진다. |
| 【0095】 FL = 5% 이하에서 단일 공정에 대한 곡선은 FL 〉 5%의 경우의 아르키메데스 수에 대해 허용되는 범위를 벗어나지 않도록 하는 범위에 있어야 하는 것으로 나타나고 있다. |
| 【0096】 시험된 모든 공정에서, 적어도 FL = 5% 까지는, 프로파일이 하강하는 양상을 나타내며, 그보다 높은 충전 수준에서는 상이한 양상으로 나타난다. |
| 【0097】 곡선 1, 2 및 3은 아르키메데스 수에 대한 3개의 전형적인 프로파일을 보여준다. (실시예 1-3을 참조) |
| 【0098】 곡선 1 및 2에서, 아르키메데스 수가 처음에는 계속 감소한다. 이는 곡선 2의 경우에는 적어도 5%의 충전 수준까지 그러하지만, 더 높은 충전 수준, 예를 들어 곡선 1에서는 약 10%의 충전 수준까지도 지속될 수 있다. |
| 【0099】 곡선 1에서, 아르키메데스 수는 그 이후 일정하다. |
| 【0100】 곡선 2에서는 전혀 다른 프로파일이 나타난다. 아르키메데스 수는 FL = 5%부터 다시 상승한다. 도 1에서는, 이중- 로그 그래프가 선택되었기 때문에 이것은 다시 지수 함수를 나타낸다. |
| 【0101】 곡선 3에서, 아르키메데스 수는 약 7%의 충전 수준까지는 감소한다. 충전 수준이 약 4%와 약 7%의 사이인 경우에, 아르키메데스 수는 충전 수준이 약 4% 보다 낮은 때에 비해 더 크게 떨어진다. 그러므로, 약 4%의 충전 수준까지는 아르키메데스 수의 프로파일은 지수 x₁의 지수 함수이고, 마찬가지로 약 4%와 약 7% 사이의 아르키메데스 수의 프로파일은 지수 x₂의 지수 함수인데, 이때 x₂ 〈 x₁이다. 충전 수준이 약 7% 보다 커지면, 아르키메데스 수는 일정해진다. |
| 【0102】 그러므로, 아르키메데스 수의 프로파일은 충전 수준의 함수로서 매우 상이할 수 있다. 아르키메데스 수는 처음에는 감소된 다음 실질적으로 일정하거나 또는 다시 상승할 수도 있다. |
| 【0103】 본 발명에서는 아르키메데스 수가 임의의 충전 수준에 대해 곡선 5 및 6에 의해 정해지는 범위를 벗어나지 않아야 한다. |
| 【0104】 본 발명자들은 아르키메데스 수가 전술한 범위를 벗어나는 모든 공정들이 종래 기술에서 이미 알려진 바와 같은 상당한 문제점들과 관련되어 있다는 것을 알게 되었다. |
| 비교실시예 |
| 【0106】 곡선 4는 EP 2 067 744 A2에 의해 공지된 공정에 대한, 충전 수준의 함수로서의 아르키메데스 수를 나타낸다. |
| 【0107】 아르키메데스 수의 측정에 필요하지만 본 출원에 개시되지 않은 모든 파라미터들에 대해서, 전형적인 수치가 추정 또는 계산되었다. 노즐의 면적은 닫힌 노즐의 비율로부터 계산되었다. |
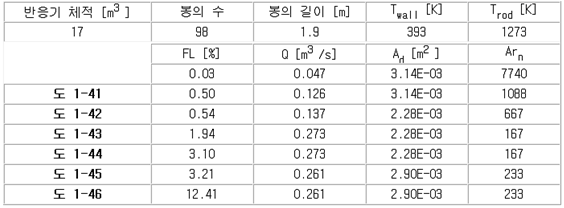
| 【0109】 포인트 41, 42, 43, 44, 45, 및 46은 도 1에 나타나 있다. |
| 【0111】 EP 2 067 744 A2에 개시된 공정에 대한 아르키메데스 수의 그래프는 본 발명의 아르키메데스 수의 범위에 못 미치며 전혀 다른 특성을 보여주고 있는데, 이는 반응 개스의 유입 속도의 변화에 기인하는 것으로 보인다. |
| 【0112】 특히, 넘어지는 봉의 비율이 증가되는 것으로 관찰된다. 증착 속도 역시 균일한 떨어지는 형태가 허용되는 때에만 충분히 높다. 아르키메데스 수의 증가가 이러한 문제들을 제거할 수 있다는 사실이 놀랍다. |
| 【0113】 DE 29 661 A1에 개시된 공정은 또한 충전 수준의 함수로서 아르키메데스 수의 그래프를 보여주고 있는데, 이것은 본 발명의 범위보다 낮다(EP 2 067 744 A2에 개시된 공정과 유사하지만, 구체적인 그래프는 없다). 이 공정에서, 이중- 제트형 노즐이 사용된다. 다음과 같은 파라미터가 사용되었다: |

| 【0115】 포인트 7은 도 1에 나타나 있다. |
| 【0116】 봉의 구조의 균일성과 관련하여 DE 29 12 661 A1에 기재된 장점이 이러한 공정에서 관찰될 수 있지만, 이 공정은 다른 단점들을 상당히 나타낸다. |
| 【0117】 예를 들어, 아르키메데스 수와 관련하여 본 발명의 범위 내에 있는 공정들 보다 비에너지 소비가 훨씬 높다. |
| 【0118】 반면, 본 발명의 공정의 경우 비에너지 소비가 10-20% 낮다. |
| 【0119】 또한, 비교 실시예의 공정에 따르면, 넘어지는 봉의 비율이 뚜렷하게 증가한다. |
| 실시예 |
| 【0122】 본 발명에 따른 3개의 상이한 공정이 제시된다. |
| 【0123】 서로 다른 반응기가 사용되었는데, 이들 반응기는 반응기의 체적 및 봉의 수에 있어서 서로 상이하다. |
| 【0124】 상기 공정들 중 하나의 공정(실시예 1)에 있어서, 48개의 봉과 12.7 m³의 체적을 가진 반응기가 사용되었다. 다른 공정(실시예 2)에서는 체적이 10 m³인 반응기에 들어 있는 24개의 봉에 대해 증착이 수행되었다. |
| 【0125】 세 번째 공정(실시예 3)에서는, 반응기 체적이 5.9 m³에 불과했고, 봉의 수는 마찬가지로 24개였다. |
| 【0126】 모든 공정에서 봉의 길이는 2.9 내지 3.1 m 였다. |
| 【0127】 표 3은 도 1에 도시된 곡선 1의 3개의 포인트 11, 12 및 13의 파라미터들을 나타낸다. |
| 【0128】 벽의 온도 Twall은 393 K로 일정했다. 노즐의 단면적은 4.185 x 10-³ ㎡로 일정했다. |
| 【0129】 두 번째 컬럼에 반응기의 충전 수준이 나타나 있다. |
| 【0130】 봉의 온도 Trod는 0.16%의 충전 수준에서 1326 K로부터 19%의 충전 수준에서 1302 K로 하강한다. |
| 【0131】 Q는 작동 조건하에서 반응 개스(트리클로로실란 및 수소)의 체적 유량을 나타내며, 그 단위는 m³/s 이다. Q는 처음에는 증가하고 그 후에는 일정하게 유지된다. |
| 【0132】 Arn은 아르키메데스 수를 나타낸다. |
| 【0133】 이 경우에, 아르키메데스 수는 10.76%의 충전 수준과 19.06%의 충전 수준 사이에서 반드시 일정하게 유지된다. 이는 또한 반응 개스의 체적 유량에도 적용되며, 0.192 m³/s로 일정하다. |

| 【0135】 표 4는 도 1에 도시된 곡선 2(실시예 2) 상의 3개의 포인트 21, 22 및 23의 파라미터들을 나타낸다. 이 경우에도 반응기의 벽의 온도 Twall은 393 K로 일정하였다. 노즐의 단면적 역시 일정하게 유지되었고, 이 경우 2.161 x 10-³ ㎡ 였다. |
| 【0136】 봉의 온도 Trod는 0.106%의 충전 수준에서 1364 K로부터 17.98%의 충전 수준에서 1306 K로 하강한다. 이 경우에 아르키메데스 수는 5.03%의 충전 수준과 17.98%의 충전 수준 사이에서 1332로부터 2671로 높아진다. |

| 【0138】 표 5는 도 1에 도시된 곡선 3(실시예 3) 상의 4개의 포인트 31, 32, 33 및 34의 파라미터들을 나타낸다. 이 경우에도 반응기의 벽의 온도 Twall은 393 K로 일정하였다. 노즐의 단면적 역시 일정하게 유지되었고, 이 경우 8.18 x 10-⁴㎡ 였다. |
| 【0139】 봉의 온도 Trod는 0.197%의 충전 수준에서 1299 K로부터 21.1%의 충전 수준에서 1233 K로 하강한다. |
| 【0140】 곡선 3(실시예 3)에서, 아르키메데스 수는 3.604%의 충전 수준과 6.5%의 충전 수준 사이에서 낮아졌는데, 충전 수준이 3.604% 보다 낮은 경우의 감소 수준에 비해 더 높은 수준으로 낮아졌다. |
| 【0141】 충전 수준 6.5%로부터 아르키메데스 수의 그래프가 일정하게 유지된다. 이때 반응기의 체적 유량도 0.058 m³/s 로 일정하게 유지된다. |

나. 선행발명들 주1)
1) 선행발명 1(갑 제12호증)
2009. 6. 2. 공개되고, 한국 공개특허공보 특2009-55511호로 게재된 ‘다결정 실리콘 제조 방법’에 관한 것이다.
2) 선행발명 2(갑 제13호증)
2010. 8. 19. 공개되고, 일본 공개특허공보에 특개2010-180078호로 게재된 ‘다결정 실리콘의 제법’에 관한 것이다.
3) 선행발명 3(갑 제14호증)
2010. 6. 15. 공개되고, 한국 공개특허공보에 특2010-65175호로 게재된 ‘다결정 실리콘 및 그의 제조 방법’에 관한 것이다.
4) 선행발명 4(갑 제15호증)
2007. 5. 8. 공개되고, 한국 공개특허공보에 특2007-48180호로 게재된 ‘결정성 규소 잉곳의 제조 방법’에 관한 것이다.
다. 이 사건 심결의 경위
1) 피고는 2017. 7. 25. 특허심판원에 원고를 상대로 하여, 이 사건 특허발명은 발명의 상세한 설명이 그 발명이 속하는 기술분야에서 통상의 지식을 가진 자(이하 ‘통상의 기술자’라고 한다)가 쉽게 실시할 수 있을 정도로 명확하고 상세하게 기재된 것이 아니고, 청구범위도 모두 명확하고 간결하게 기재되어 있지 아니하며, 선행발명 1 내지 4로부터 진보성이 부정된다는 이유로 등록무효심판을 청구하였다( 2017당2655호 ).
2) 특허심판원은 2018. 10. 10. 이 사건 특허발명은 구 특허법(2011. 5. 24. 법률 제10716호로 개정되기 전의 것) 제42조 제3항 에 위배되고, 이 사건 제1항 내지 제8항 발명은 구 특허법(2014. 6. 11. 법률 제12753호로 개정되기 전의 것) 제42조 제4항 제2호 에 위배되며, 이 사건 제1항 내지 제4항 발명은 선행발명 1에 의해, 이 사건 제5항 발명은 선행발명 1과 2에 의해, 이 사건 제6항 발명은 선행발명 1과 3에 의해, 이 사건 제7항 및 제8항 발명은 선행발명 1과 4에 의하여 각각 진보성이 부정된다는 이유를 들어 원고의 위 심판청구를 인용하는 내용의 이 사건 심결을 하였다 주2) .
[인정근거] 다툼 없는 사실, 갑 제1 내지 3, 12 내지 15호증의 각 기재, 변론 전체의 취지
2. 당사자의 주장
가. 원고 주장의 요지
이 사건 특허발명은 다음과 같이 통상의 기술자가 발명의 상세한 설명에 의해 쉽게 실시할 수 있을 정도로 명확하고 상세하게 기재되어 있고, 청구범위도 모두 명확하고 간결하게 기재되어 있으며, 선행발명들 등에 대해 신규성 및 진보성을 모두 충족하고 있으므로, 아무런 무효사유도 존재하지 않는다. 그럼에도 불구하고 이와 결론을 달리 한 이 사건 심결은 위법하다.
1) 이 사건 특허발명에 정의된 아르키메데스 수(이하 ‘이 사건 아르키메데스 수’라 한다)의 유도과정이 반드시 이 사건 특허발명 명세서(이하 ‘이 사건 명세서’라 한다)에 기재될 필요는 없고, 이 사건 아르키메데스 수에 기술적 오류나 모순은 존재하지 않으며, 이 사건 아르키메데스 수와 이 사건 특허발명의 효과 사이의 인과관계 역시 이 사건 명세서에 명확하게 기재되어 있다.
2) 통상의 기술자라면 이 사건 명세서의 기재를 통해 이 사건 아르키메데스 수 및 충전수준(Fill Level : FL)을 구성하는 모든 공정변수의 의미, 측정 기준 및 방법을 명확히 이해할 수 있으므로, 이 사건 특허발명은 발명의 상세한 설명에 용이하게 실시할 수 있을 정도로 명확하고 상세하게 기재되어 있고, 청구범위도 모두 명확하고 간결하게 기재되어 있다.
3) 이 사건 특허발명은 수치범위 내외에서 임계적 의의가 필요한 수치한정 발명이라고 볼 수 없고, 선행발명들에는 이 사건 아르키메데스 수와 관련한 구성요소 4, 5에 대응하는 구성이 전혀 포함되어 있지 아니하므로, 선행발명들에 의해 진보성이 부정되지 아니한다.
4) 한편, 피고는 ‘별건 침해소송( 서울중앙지방법원 2017가합509596 , 이하 ‘관련 침해소송’이라 한다)에서의 원고 주장, 즉 피고가 SDR 400 반응기를 사용하여 연간 400톤의 다결정 실리콘을 생산하는 경우 이 사건 특허발명의 제조방법을 침해할 수밖에 없다는 원고의 주장이 옳다면, 피고는 이 사건 특허발명의 우선일 이전에 이미 SDR 400 반응기를 도입하여 운용하였으므로, 이 사건 특허발명은 피고의 SDR 400 반응기 운용에 의해 신규성을 상실한 것’이라고 주장하나, 위와 같은 가정적 판단에 근거한 신규성 상실 주장은 법리상 가능하지 아니할 뿐만 아니라, 이를 증명할 아무런 증거도 없다.
나. 피고 주장의 요지
이 사건 특허발명은 다음과 같이 통상의 기술자가 발명의 상세한 설명에 의해 쉽게 실시할 수 있을 정도로 명확하고 상세하게 기재되어 있지 아니하고, 청구범위도 명확하고 간결하게 기재되어 있지 아니하며, 선행발명들 등에 비해 신규성 및 진보성도 모두 인정되지 아니하므로, 그 등록이 무효로 되어야 한다. 따라서 이와 결론을 같이 한 이 사건 심결은 적법하다.
1) 이 사건 아르키메데스 수의 기술적 의의 및 효과와의 관계가 이 사건 명세서에 기재되어 있지 않고, 출원 이후 원고가 밝힌 이 사건 아르키메데스 수의 유도과정에 관한 자료를 참작하여 보더라도 그 유도과정에 과학적·기술적 오류가 있으므로, 통상의 기술자는 여전히 이 사건 아르키메데스 수의 기술적 의의 및 효과를 이해할 수 없다.
2) 이 사건 아르키메데스 수를 구성하는 변수들 중 봉의 길이(L), 봉의 온도(Trod), 벽의 온도(Twall) 및 유량(Q)과 충전수준(FL)은 의미가 불분명하거나, 이 사건 명세서에 그 측정을 위한 기준, 방법 및 조건에 대한 설명이 명확하게 기재되어 있지 않으므로, 이 사건 특허발명은 이 사건 명세서 기재에 의해 용이하게 실시될 수 없고, 청구범위도 명확하고 간결하게 기재되어 있지 않다.
3) 이 사건 제1항 발명의 구성요소 1 내지 3은 선행발명 1에 명시적으로 개시되어 있고, 구성요소 4, 5는 선행발명 1에 내재되어 있는 구성이거나 단순 수치한정에 해당하여 임계적 의의가 인정될 수 없으므로, 이 사건 제1항 발명은 통상의 기술자가 선행발명 1로부터 용이하게 도출할 수 있다.
4) 한편, 원고는 관련 침해소송에서 ‘피고가 SDR 400 반응기를 사용하여 연간 400톤의 다결정 실리콘을 생산하는 경우 이 사건 특허발명의 제조방법을 침해할 수밖에 없다’고 주장하였는데, 원고의 위 주장이 옳다면, 피고는 이 사건 특허발명의 우선일 이전에 이미 SDR 400 반응기를 도입하여 운용한 것이므로, 이 사건 특허발명은 피고의 SDR 400 반응기 운용에 의해 신규성을 상실하였다.
3. 이 사건 특허발명의 ‘발명의 상세한 설명’ 기재불비에 대한 판단
가. 관련 규정 및 판단 기준
1) 구 특허법 제42조 제3항 제1호 는 발명의 상세한 설명의 기재가 “그 발명이 속하는 기술분야에서 통상의 지식을 가진 자가 그 발명을 쉽게 실시할 수 있도록 지식경제부령이 정하는 기재방법에 따라 명확하고 상세하게 기재”되어 있어야 한다고 규정하고, 그에 따라 구 특허법 시행규칙(2014. 12. 30. 산업통상자원부령 제103호로 개정되기 전의 것) 제21조 제3항 은 “발명의 상세한 설명에는 기술분야, 해결하고자 하는 과제, 과제의 해결 수단, 그 밖에 그 발명이 속하는 기술분야에서 통상의 지식을 가진 자가 그 발명의 내용을 쉽게 이해하기 위하여 필요한 사항을 포함하여야 한다.”라고 규정하고 있다. 이때 위 조항들에서 요구하는 명세서 기재의 정도는 통상의 기술자가 출원 시의 기술 수준으로 보아 과도한 실험이나 특수한 지식을 부가하지 않고서도 명세서의 기재에 의하여 당해 발명을 정확하게 이해할 수 있고 동시에 재현할 수 있는 정도를 말한다( 대법원 2011. 10. 13. 선고 2010후2582 판결 취지 등 참조). 한편, 일반적으로 기계장치 등에 관한 발명에 있어서는 특허출원의 명세서에 실시예가 기재되어 있지 않더라도 당업자가 발명의 구성으로부터 그 작용과 효과를 명확하게 이해하고 용이하게 재현할 수 있는 경우가 많으나, 이른바 실험의 과학이라고 하는 화학발명의 경우에는 당해 발명의 내용과 기술 수준에 따라 차이가 있을 수는 있지만 예측가능성 내지 실현가능성이 현저히 부족하여 실험데이터가 제시된 실험예가 기재되어 있지 않으면 당업자가 그 발명의 효과를 명확하게 이해하고 용이하게 재현할 수 있다고 보기 어려워서 완성된 발명으로 보기 어려운 경우가 많고( 대법원 2001. 11. 30. 선고 2000후2958, 2001후65 판결 등 참조), ‘물건을 생산하는 방법의 발명’의 경우 그 발명의 ‘실시’라고 함은 그 방법을 사용하는 등의 행위를 말하므로, 그 발명의 특허청구범위에 특정된 방법 전체의 사용 등에 관하여 위와 같은 정도의 명세서 기재가 없는 경우에는 발명의 상세한 설명에 대한 기재요건을 충족한다고 볼 수 없다. 따라서 구성요소의 범위를 수치로써 한정하여 표현한 ‘물건을 생산하는 방법의 발명’에서도 그 특허청구범위에 한정된 수치범위 전체를 보여주는 실시례까지 요구되는 것은 아니지만, 통상의 기술자가 출원 시의 기술 수준으로 보아 과도한 실험이나 특수한 지식을 부가하지 않고서는 명세서의 기재만으로 위 수치범위 전체에 걸쳐 그 생산 방법을 사용할 수 없는 경우에는, 위 조항에서 정한 기재요건을 충족하지 못한다고 보아야 한다( 대법원 2015. 9. 24. 선고 2013후525 판결 취지 참조). 나아가 위와 같은 규정 및 법리는 종래 사용되지 않았던 성질 또는 특성 등에 의해 물(물) 또는 그 제조방법을 특정하려고 하는 기재를 포함하는 특허발명인 이른바 파라미터발명의 경우에도 마찬가지로 적용된다 할 것인바, 통상의 기술자가 출원 시의 기술 수준으로 보아 과도한 실험이나 특수한 지식을 부가하지 아니하고서도 명세서의 기재에 의하여 새로운 파라미터의 의미, 그 측정 방법 등을 포함한 발명 전체의 구성 및 효과를 정확하게 이해할 수 있고 동시에 재현할 수 있어야 한다.
2) 이 사건 특허발명은 지멘스 반응기 내에서 화학 반응을 통해 실리콘 증착을 일으켜 다결정 실리콘을 제조하는 방법에 관한 화학발명인 동시에, 이 사건 명세서 기재를 통해 새롭게 정의된 “반응기의 공부피(empty volume)에 대한 봉의 부피의 비(백분율)를 의미하는 충전수준(FL)”과 “반응기 내 유동조건(flow condition)을 나타내는 아르키메데스 수(Arn)” 사이의 상관관계를 연산식과 수치로 한정한 파라미터발명에 해당한다. 따라서 이 사건 특허발명이 발명의 상세한 설명에 대한 기재요건을 충족하기 위해서는 통상의 기술자가 출원 시의 기술 수준으로 보아 과도한 실험이나 특수한 지식을 부가하지 아니하고서도 이 사건 명세서의 기재에 의하여 새로운 파라미터를 포함한 이 사건 특허발명의 모든 구성을 특허청구범위에서 한정한 수치범위 전체에 걸쳐 정확히 이해함으로써 이를 사용할 수 있고, 위 구성으로부터 얻어지는 효과 역시 위 수치범위 전체에 걸쳐 이 사건 명세서에서 구체적인 실험, 실시예 등으로 증명되거나 통상의 기술자가 출원 시 기술 수준으로 보아 이를 능히 예측할 수 있어야 한다.
나. 판단
1) 이 사건 제1항 발명 주3) 을 통상의 기술자가 사용할 수 있는지 여부(발명의 구성에 대한 이해 및 재현 여부)
가) 명세서 관련 기재 및 쟁점
(1) 이 사건 명세서 기재 내용 중 이 사건 제1항 발명의 기술적 수단, 즉 구성에 관한 주요 내용은 아래와 같다.
| 과제의 해결 수단 |
| 【0053】 본 발명의 전술한 목적은 본 발명의 다결정 실리콘의 제조 방법(구성요소 1)에 의해 달성되는데, 상기 방법은, 실리콘- 함유 성분 및 수소를 포함하는 반응 개스를 하나 이상의 노즐에 의해 반응기에 도입하는 단계를 포함하며(구성요소 2), 상기 반응기는 실리콘이 증착되는 하나 이상의 가열되는 필라멘트 봉을 포함하며(구성요소 3), 반응기의 공부피(empty volume)에 대한 봉의 부피의 비(백분율)를 의미하는 충전 수준(fill level: FL)의 함수로서(구성요소 4) 반응기내 유동 조건을 나타내는 아르키메데스 수(Archimedes number: Arn)가 5%까지의 충전 수준 FL에 대해서는 함수 Ar = 2000 x FL-0.6에 의한 하한값과 함수 Ar = 17000 x FL-0.9에 의한 상한값으로 정해지는 범위 내이며, 충전 수준 FL이 5% 보다 큰 경우에는 750 내지 4000인 것(구성요소 5)을 특징으로 한다주4). |
| 【0054】 공정의 성공을 위해서는, 강제 대류(forced convection)에 대한 자유 대류(free convection)의 비로서 반응기 내 유동 조건을 의미하는 아르키메데스 수가 정해진 범위 내에 존재하도록 공정을 수행하는 것이 필수적이다. 이 범위는 전체 공정 기간에 대해 정해진다. |
| 【0055】 이러한 목적을 위해, 아르키메데스 수는 반응기의 충전 수준의 함수로서 보고되어 있다. |
| 【0056】 반응기의 충전 수준은 반응기의 공부피에 대한 봉의 부피의 비(백분율)를 의미한다. 반응기의 공부피는 일정하다. |
| 【0057】 그러므로 공정 기간이 증가하면 봉의 부피가 증가하기 때문에 충전 수준이 증가한다. |
| 【0058】 상기 공정과 아르키메데스 수에 대한 본 발명의 범위는 반응기의 크기와 관계 없다. 그러므로 상기 공정은 작은 반응기와 큰 반응기 모두에 대해 적절하게 적용된다. |
| 【0059】 마찬가지로, 상기 공정은 반응기에 존재하는, 실리콘이 증착되는 필라멘트 봉의 수 및 길이와는 관계없다. |
| 【0060】 아르키메데스 수에 의한 용기 내 유동 조건에 대한 일반적인 설명은 엔지니어링 열역학 텍스트북(예: Dittmann/Fischer/Huhn/Klinger, "Repetitorium der technischen Thermodynamik" [Refresher in Engineering Thermodynamics], Teubner Verlag (1995))에 공지되어 있다. |
| 【0061】 아르키메데스 수는 또한 "리차드슨 수(Richardson number)로도 알려져 있다. |
| 【0062】 다결정 실리콘의 증착을 위한 지멘스 반응기에 대해서는 아르키메데스 수와 관련하여 아직 아무런 평가가 이루어져 있지 않다. |
| 【0063】 실리콘의 증착에 사용되는 지멘스 반응기는 소정의 부피(공부피)를 가진 용기로서 간주될 수 있는데, 상기 부피는 특정 온도 Twall를 가진 벽에 의해 한정된다. 또한, 이 공간은 실리콘의 증착 결과 시간이 경과함에 따라 성장하며 특정 온도 Trod를 가진 봉을 수납한다. |
| 【0064】 개스는 가열된 봉에서 가열되어 상방으로 올라간다. 벽에서 개스가 다시 냉각되고 하방으로 내려온다. 이 과정을 개스의 자유 대류라고 한다. |
| 【0065】 또한, 반응 개스(수소 및 실리콘을 함유하는 개스로서, 예를 들어 트리클로로실란과 디클로로실란의 혼합물)는 일반적으로 베이스에 장착된 노즐에 의해 정해진 유입 속도로 이 공간으로 능동적으로 유입된다. 이것이 강제 대류를 야기한다. |
| 【0066】 동시에 방출 개스가 용기로부터 방출되고 용기 내 압력이 전형적으로는 일정하게 유지된다. |
| 【0067】 자유 대류는 부력에 기인하고, 강제 대류는 관성력에 기인한다. 이러한 2개의 유동력의 상호 작용이 외관상으로는 복잡한 유동 조건과 반응기 내 증착에 대한 그 효과를 지배하는 것으로 나타났다. 그러므로, 관성력에 대한 부력의 비로서 정의되는 아르키메데스 수가 유동 조건을 특성화하는 데 적합하다. |
| 【0068】 지멘스 반응기에서 봉에 대한 아르키메데스 수의 구체적인 유도 방법에 대해서는 여기서는 다시 설명하지 않기로 한다. |
| 【0069】 그 결과는 다음 관계식으로 표시된다: |
| 【0070】 Ar = Π * g * L³ * Ad * (Trod - Twall) / (2 * Q² * (Trod + Twall)) |
| 【0071】 상기 식에서, g는 중력으로 인한 가속도이고 그 단위는 m/s²이며, L은 필라멘트 봉의 길이이고 그 단위는 m이며, Q는 작동 조건(p, T) 하에서 개스의 체적 유량(volume flow)이며, 그 단위는 m³/s이고, Ad는 모든 노즐의 단면적의 합이며, 그 단위는 ㎡이고, Trod는 봉의 온도이고 그 단위는 K이며, Twall은 벽의 온도이고 그 단위는 K이다. |
| 【0072】 필라멘트 봉의 길이는 증착 기간 동안에, 예를 들어 L = 3m와 같이 반드시 일정하게 유지된다. |
| 【0073】 반응기가 반응 개스의 주입을 위해 동일 또는 상이한 단면을 가진 하나 이상의 노즐을 포함하는 경우, 모든 노즐의 단면적의 합 Ad(단위: ㎡)을 고려한다. 하나 또는 그 이상의 노즐의 단면적은 시간이 경과함에 따라 달라질 수도 있다. |
| 【0074】 모든 단면적의 합 Ad는 바람직하기로는 5 x 10-5㎡ 내지 약 1x 10-²㎡ 이다. |
| 【0075】 봉의 온도는 바람직하기로는 1150 K 내지 1600 K 이다. |
| 【0076】 벽의 온도는 바람직하기로는 300 K 내지 700 K 이다. |
| 【0077】 체적 유량은 바람직하기로는 작동 조건하에서 0.001m³/s 내지 0.5m³/s 이다. |
| 【0078】 하나의 반응기에 여러 개의 필라멘트 봉이 들어 있는 경우에는, 아르키메데스 수는 이들 봉의 수 n에 대한 합으로서 결정된다. 그 결과는 Arn 이다. |
| 【0079】 그 식은 다음과 같다: |
| 【0080】 Arn = n * Ar |
| 【0081】 그러나, 본 발명에 따른 공정은 이미 앞서 언급한 바와 같이 반응기 내의 봉의 수와 관계가 없다. |
| 【0082】 (선략) 봉의 수를 두 배로 증가시키는 경우에 최적 공정은 다시 본 발명에 따른 공정에서 청구된 유동 조건에 대응하는 유동 조건을 필요로 한다. |
| 【0083】 아르키메데스 수가, 5%까지의 충전 수준 FL에 대해서는 함수 Ar = 2000 x FL-0.6 에 의한 하한값과 함수 Ar = 17000 x FL-0.9에 의한 상한값으로 정해지는 범위 내이고, 충전 수준 FL이 5% 보다 큰 경우에는 750 내지 4000의 범위 내인 모든 공정의 경우에, 다음과 같은 유리한 기술적인 효과가 동시적으로 및 반복적으로 발생한다. |
| 【0086】 본 발명의 명세서에 있어서, 봉의 온도는 수직 봉의 표면, 바람직하기로는 반응기의 외벽에 가장 가까운 봉의 측면에서, 봉의 높이의 중간 지점에서 방사선 고온계에 의해 측정된다. 따라서, 표면 온도는 봉의 중간 지점에서 조절된다. (후략) |
| 발명의 실시를 위한 구체적인 내용 |
| 【0092】 도 1은 충전 수준의 함수로서 아르키메데스 수의 바람직한 범위를 나타낸다. 곡선이 이중- 로그 형태(double-logarithmic form)로 나타나 있다. |
| 【0093】 본 발명의 범위는 아르키메데스 수의 최대 및 최소 프로파일을 보여주는 라인 5와 6으로 나타나 있다. FL = 5% 까지는, 이들 라인은 지수 함수를 나타낸다. |
| 【0094】 FL = 5% 이하에서는, 두 개의 곡선 5와 6의 기울기는 이중- 로그 그래프에서 서로 상이하다. 따라서 두 개의 지수 함수는 상이한 지수를 가진다. |
| 【0095】 FL = 5% 이하에서 단일 공정에 대한 곡선은 FL 〉 5%의 경우의 아르키메데스 수에 대해 허용되는 범위를 벗어나지 않도록 하는 범위에 있어야 하는 것으로 나타나고 있다. |
| 【0096】 시험된 모든 공정에서, 적어도 FL = 5% 까지는, 프로파일이 하강하는 양상을 나타내며, 그보다 높은 충전 수준에서는 상이한 양상으로 나타난다. |
| 【0097】 곡선 1, 2 및 3은 아르키메데스 수에 대한 3개의 전형적인 프로파일을 보여준다. (실시예 1-3을 참조) |
| 【0098】 곡선 1 및 2에서, 아르키메데스 수가 처음에는 계속 감소한다. 이는 곡선 2의 경우에는 적어도 5%의 충전 수준까지 그러하지만, 더 높은 충전 수준, 예를 들어 곡선 1에서는 약 10%의 충전 수준까지도 지속될 수 있다. |
| 【0099】 곡선 1에서, 아르키메데스 수는 그 이후 일정하다. |
| 【0100】 곡선 2에서는 전혀 다른 프로파일이 나타난다. 아르키메데스 수는 FL = 5%부터 다시 상승한다. 도 1에서는, 이중- 로그 그래프가 선택되었기 때문에 이것은 다시 지수 함수를 나타낸다. |
| 【0101】 곡선 3에서, 아르키메데스 수는 약 7%의 충전 수준까지는 감소한다. 충전 수준이 약 4%와 약 7%의 사이인 경우에, 아르키메데스 수는 충전 수준이 약 4% 보다 낮은 때에 비해 더 크게 떨어진다. 그러므로 약 4%의 충전 수준까지는 아르키메데스 수의 프로파일은 지수 x₁의 지수 함수이고, 마찬가지로 약 4%와 약 7% 사이의 아르키메데스 수의 프로파일은 지수 x₂의 지수 함수인데, 이때 x₂ 〈 x₁ 이다. 충전 수준이 약 7% 보다 커지면, 아르키메데스 수는 일정해진다. |
| 【0102】 그러므로, 아르키메데스 수의 프로파일은 충전 수준의 함수로서 매우 상이할 수 있다. 아르키메데스 수는 처음에는 감소된 다음 실질적으로 일정하거나 또는 다시 상승할 수도 있다. |
| 실시예 |
| 【0122】 본 발명에 따른 3개의 상이한 공정이 제시된다. |
| 【0123】 서로 다른 반응기가 사용되었는데, 이들 반응기는 반응기의 체적 및 봉의 수에 있어서 서로 상이하다. |
| 【0124】 상기 공정들 중 하나의 공정(실시예 1)에 있어서, 48개의 봉과 12.7 m³의 체적을 가진 반응기가 사용되었다. 다른 공정(실시예 2)에서는 체적이 10 m³인 반응기에 들어 있는 24개의 봉에 대해 증착이 수행되었다. |
| 【0125】 세 번째 공정(실시예 3)에서는, 반응기 체적이 5.9 m³에 불과했고, 봉의 수는 마찬가지로 24개였다. |
| 【0126】 모든 공정에서 봉의 길이는 2.9 내지 3.1 m 였다. |
| 【0127】 표 3은 도 1에 도시된 곡선 1의 3개의 포인트 11, 12 및 13의 파라미터들을 나타낸다. |
| 【0128】 벽의 온도 Twall은 393 K로 일정했다. 노즐의 단면적은 4.185 x 10-³㎡로 일정했다. |
| 【0129】 두 번째 컬럼에 반응기의 충전 수준이 나타나 있다. |
| 【0130】 봉의 온도 Trod는 0.16%의 충전 수준에서 1326 K로부터 19%의 충전 수준에서 1302 K로 하강한다. |
| 【0131】 Q는 작동 조건하에서 반응 개스(트리클로로실란 및 수소)의 체적 유량을 나타내며, 그 단위는 m³/s 이다. Q는 처음에는 증가하고 그 후에는 일정하게 유지된다. |
| 【0132】 Arn은 아르키메데스 수를 나타낸다. |
| 【0133】 이 경우에, 아르키메데스 수는 10.76%의 충전 수준과 19.06%의 충전 수준 사이에서 반드시 일정하게 유지된다. 이는 또한 반응 개스의 체적 유량에도 적용되며, 0.192 m³/s로 일정하다. |

| 【0135】 표 4는 도 1에 도시된 곡선 2(실시예 2) 상의 3개의 포인트 21, 22 및 23의 파라미터들을 나타낸다. 이 경우에도 반응기의 벽의 온도 Twall은 393 K로 일정하였다. 노즐의 단면적 역시 일정하게 유지되었고, 이 경우 2.161 x 10-³ ㎡ 였다. |
| 【0136】 봉의 온도 Trod는 0.106%의 충전 수준에서 1364 K로부터 17.98%의 충전 수준에서 1306 K로 하강한다. 이 경우에 아르키메데스 수는 5.03%의 충전 수준과 17.98%의 충전 수준 사이에서 1332로부터 2671로 높아진다. |

| 【0138】 표 5는 도 1에 도시된 곡선 3(실시예 3) 상의 4개의 포인트 31, 32, 33 및 34의 파라미터들을 나타낸다. 이 경우에도 반응기의 벽의 온도 Twall은 393 K로 일정하였다. 노즐의 단면적 역시 일정하게 유지되었고, 이 경우 8.18 x 10-4㎡ 였다. |
| 【0139】 봉의 온도 Trod는 0.197%의 충전 수준에서 1299 K로부터 21.1%의 충전 수준에서 1233 K로 하강한다. |
| 【0140】 곡선 3(실시예 3)에서, 아르키메데스 수는 3.604%의 충전 수준과 6.5%의 충전 수준 사이에서 낮아졌는데, 충전 수준이 3.604% 보다 낮은 경우의 감소 수준에 비해 더 높은 수준으로 낮아졌다. |
| 【0141】 충전 수준 6.5%로부터 아르키메데스 수의 그래프가 일정하게 유지된다. 이때 반응기의 체적 유량도 0.058 m³/s 로 일정하게 유지된다. |

(2) 통상의 기술자가 이 사건 제1항 발명인 다결정 실리콘의 제조방법을 이 사건 명세서의 기재를 통해 용이하게 사용하기 위해서는, 우선 이 사건 제1항 발명의 모든 구성요소를 정확히 이해하고, 이를 재현할 수 있어야 하는데, 위 구성요소들 중 구성요소 1 내지 3이 종래 공지된 지멘스 공정에 관한 것으로서 통상의 기술자가 명세서 및 도면에 기재된 사항과 출원 시의 기술 상식에 기초하여 이들을 정확히 이해하고 쉽게 재현할 수 있음은 기록상 명확하고, 당사자 사이에 다툼도 없다. 따라서 이 사건 제1항 발명인 제조방법의 용이 사용 가능 여부는 통상의 기술자에 의한 구성요소 4, 5의 이해 및 재현 여부에 좌우된다 할 것이고, 이는 구체적으로 구성요소 4, 5에 포함된 공정변수들이 무엇을 의미하는지, 그 측정 기준 및 방법이 무엇인지를 통상의 기술자가 이 사건 명세서 및 도면에 기재된 사항과 출원 시의 기술 상식에 기초하여 정확히 이해하고 재현할 수 있는지 여부에 관한 것이므로, 이하 차례로 살펴본다.
나) 구성요소 4[충전수준(FL)]에 포함된 봉의 부피(Vrod)
(1) 이 사건 명세서에서 구성요소 4인 충전수준(FL)은 ‘반응기의 공부피(empty volume, Vreactor)에 대한 봉의 부피(Vrods)비’를 의미한다고 규정하고 있는바, 이때 ‘봉’은 (i) ‘충전 수준’이라는 용어 자체가 실리콘으로 반응기가 채워지는 공정, 즉 실리콘 증착 반응이 이루어지는 공정의 개시를 전제로 하고 있는 점, (ii) 이 사건 명세서 전체에 걸쳐 위 증착 반응이 진행된 단계에서의 ‘봉’ 또는 ‘실리콘 봉(또는 폴리실리콘 주5) 봉)’이라는 용어를, 실리콘 증착 반응이 진행되기 전의 ‘필라멘트 봉’ 또는 그와 수직 방향으로 연결된 ‘브릿지’와 구분하여 사용하고 있는 점(식별번호 [0007] 내지 [0045], [0059] 내지 [0059], [0071] 등 참조) 등에 비추어 볼 때 ‘필라멘트 봉’ 또는 ‘브릿지’와 구분되는 의미에서의 ‘실리콘 봉’, 즉 실리콘 증착 반응이 진행된 단계에서의 ‘실리콘 봉’을 의미하는 것으로 보인다. 그런데 이 사건 명세서에는 위와 같이 증착 반응이 진행 중인 상태에 있는 실리콘 봉의 부피(Vrods)를 측정하는 방법, 나아가 그로부터 계산되는 충전수준(FL)의 측정 방법에 대해 별다른 기재가 없다.
(2) (가) 이에 대하여 원고는, ① 이 사건 명세서에서 봉의 형태를 원기둥으로 간주하고 있고, 당해 기술 분야에서 봉의 형태를 원기둥으로 보고 봉의 부피를 계산하는 것은 통상적으로 사용되는 방법이며, ② 반응 초기부터 반응이 진행되는 동안 실리콘 봉의 모양을 원기둥 모양으로 간주하는 것은 당해 기술 분야에서 통상의 기술 상식이고, ③ 실제 반응 중 실리콘 봉의 지름인 D가 축 방향으로 크게 변하지 않아 관측 창을 통한 한 지점의 실리콘 봉 지름 측정으로도 Vrods의 측정이 가능하며, ④ 실제 반응 중 실리콘 봉의 길이는 유의미하게 성장하지 않아 실리콘 봉의 길이 방향 성장을 Vrods의 측정에 반영할 필요가 없으므로, 통상의 기술자는 이 사건 명세서에 Vrods의 측정 방법이 기재되어 있지 않다 하더라도 Vrods를 용이하게 이해하여 측정할 수 있다고 주장한다.
(나) 우선 위 ① 주장에 관하여 살피건대, 이 사건 명세서의 배경기술 부분에 ‘증착 공정 동안 실리콘 봉의 구조는 이상적으로는 커지는 반경의 실린더에 대응한다. 이러한 실린더 형태에서 일탈하면 공정에 혼란이 야기될 수 있다.’(식별번호 [0031])는 내용이 기재되어 있는 사실은 인정되나, 위와 같은 배경기술로서의 이상적 증착 공정을 설명하는 기재만으로는 통상의 기술자가 이 사건 제1항 발명의 Vrods를 측정함에 있어 반응 공정 동안의 실리콘 봉이 원기둥으로 간주되는 것임을 인식할 수 있다고 보기 어렵다.
또한 관련 선행 기술문헌들에, 실리콘 봉의 형태를 ‘증착 만드렐(mandrel, 원기둥)’로 표현하면서 그 실리콘 봉의 전체 표면적을 ‘만드렐’의 지름 및 길이를 통해 계산하는 내용(갑 제17호증), 봉의 ‘직경’이 증가함에 따라 실리콘 증착 표면을 일정 온도로 유지하는데 필요한 전류가 점차 증가한다는 내용(갑 제18호증), 봉의 ‘직경’이 증가함에 따라 전류와 전압이 변한다는 내용(갑 제19호증), CVD 공정 동안 실리콘 봉의 ‘직경’이 커진다는 내용(갑 제20호증), 실리콘 봉의 ‘직경’이 증가할 때 전류 공급이 증가되어야 한다는 내용(갑 제21호증), 실리콘 로드 주6) 의 표면적 계측 방법으로, 가스 크로마토그래프의 조성 분석을 통해 생성된 실리콘의 양과 필라멘트 봉의 길이에서 로드 ‘직경’을 산출하고 표면적을 계산하는 방법과, 관측 창으로부터 실리콘 로드의 ‘직경’을 직접 측정함에 의해 계산하는 방법이 있다는 내용(갑 제22호증), 실리콘 생산량은 실리콘 봉의 ‘직경’에 대응하므로 조업 중 실리콘 봉의 ‘직경’ 추이를 아는 것이 중요하다는 내용(갑 제23호증), 폴리실리콘 봉을 ‘원기둥’으로 형상화한 시스템을 개시하는 내용(갑 제24호증), 전기저항가열 및 Si 석출이 계속되면 Si 막대 주7) (rod)의 ‘직경’이 증가한다는 내용(갑 제25호증), 지멘스법에 있어서 종결정으로서 사용되는 ‘직경’ 10mm의 Si 로드가 1주일의 반응으로 ‘직경’ 200 ~ 250 mm 정도까지 성장한다는 내용(갑 제26호증)이 기재되어 있는 사실이 인정되는바(한편, 원고는 갑 제41호증도 그 주장의 근거로 삼고 있으나, 갑 제41호증은 이 사건 제1항 발명의 출원일 이후인 2016. 4. 4.에 공개된 문헌이므로, 이 사건 제1항 발명 출원 시 통상의 기술자의 인식 정도를 증명하는 자료로 보기는 어렵다), 위 기재 내용들에서 ‘원기둥’이라는 표현, 나아가 봉의 단면이 원임을 전제로 ‘(원의) 직경’이라는 표현이 사용됨으로써 실리콘 봉의 형태가 원기둥임을 나타내고 있다고 보이기는 한다. 그러나 위 기재 부분들의 구체적 내용에 비추어 볼 때, 이들은 위 관련 기술문헌들의 해당 내용 설명에 대한 각각의 필요에 따라 실리콘 봉의 형태가 원기둥으로 간주되어 설명된 경우들이 있다는 사실만을 의미하는 것일 뿐, 원고가 주장하는 바와 같이 통상의 기술자가 반응 중 실리콘 봉의 부피를 측정함에 있어 실리콘 봉을 원기둥으로 간주한 후 일반적인 원기둥의 부피 계산방법을 통해 그 부피를 추정하는 것이 통상적으로 인정되는 기술 상식임을 의미하는 것이라고 볼 수 없다. 더구나 아래와 같은 이 사건 제1항 발명의 특성을 고려하여 보면, 이 사건 제1항 발명의 Vrods 측정시 통상의 기술자가 이 사건 명세서상 특별한 기재 없이도 반응 중 실리콘 봉을 원기둥으로 간주한 후 일반적인 원기둥의 부피 계산방법을 통해 그 부피를 추정하여 그 추정치를 Vrods로 사용할 것이라고 기대할 수 없음이 명확하다 할 것인바, 이에 대하여는 항을 바꾸어 살펴본다.
(다) 이 사건 명세서에는 ‘(본 발명의) 상기 방법은 (중략) 반응기의 공부피에 대한 봉의 부피의 비(백분율)를 의미하는 충전 수준의 함수로서 반응기 내 유동 조건을 나타내는 아르키메데스 수가 (연산식 및 수치에 관한 설명 중략) 750 내지 4000 인 것을 특징 으로 한다(식별번호[0053])’, ‘(이 사건 제1항 발명을 통한 실리콘 반응) 공정의 성공을 위해서는, 강제 대류(forced convection)에 대한 자유 대류(free convection)의 비로서 반응기 내 유동 조건을 의미하는 아르키메데스 수가 정해진 범위 내에 존재하도록 공정을 수행하는 것이 필수적 이다. 이 범위는 전체 공정 기간 에 대해 정해진다(식별번호 [0054])’, ‘자유 대류는 부력에 기인하고, 강제 대류는 관성력에 기인한다. 이러한 2개의 유동력의 상호 작용이 외관상으로는 복잡한 유동 조건과 반응기 내 증착에 대한 그 효과를 지배 하는 것으로 나타났다. 그러므로 관성력에 대한 부력의 비로서 정의되는 아르키메데스 수가 유동 조건을 특성화하는 데 적합하다(식별번호 [0067])’, ‘ Ar = Π * g * L³ * Ad * (Trod - Twall) / (2 * Q² * (Trod + Twall)) . 상기 식에서, g는 중력으로 인한 가속도이고 그 단위는 m/s²이며, L 은 필라멘트 봉의 길이이고 그 단위는 m이며, Q 는 작동 조건(p, T) 하에서 개스의 체적 유량(volume flow)이며, 그 단위는 m³/s이고, Ad 는 모든 노즐의 단면적의 합이며, 그 단위는 ㎡이고, Trod 는 봉의 온도이고 그 단위는 K이며, Twall 은 벽의 온도이고 그 단위는 K이다(식별번호 [0071], [0072])’라고 기재되어 있는바, 이에 비추어 보면, 이 사건 제1항 발명의 기술적 사상은 위 각 공정변수가 반응 중 계속하여 서로 밀접한 영향을 주고받아 반응기 내 유동 조건을 결정함을 전제로 하여 반응 중 각 공정변수의 연동된 조절을 통해 반응기 내 유동 조건을 일정 범위 내로 존재시키고, 그 결과 반응기 내 실리콘 증착 공정이 최적화되는 효과가 나타날 수 있음을 그 중심적 특징으로 하고 있다.
따라서 이 사건 제1항 발명은 위와 같이 반응 중 각 공정변수의 상호 연동된 실제 조절이 중시되는 발명 내용의 본질상 ‘반응 중 공정변수의 실제 측정치’가 이 사건 제1항 발명의 구성 및 작용·효과의 구현에 매우 중요한 기능을 수행하는 특징을 갖고 있다 할 것인데, 이 사건 명세서에 공정변수 중 하나인 Vrods의 측정 방법에 관해 별다른 기재가 없음은 앞서 본 바와 같은바, 이 경우 통상의 기술자가 이 사건 제1항 발명인 제조방법을 실제 사용함에 있어 Vrods를 반응 중 실측치가 아닌 추정치로 적용하더라도 이 사건 제1항 발명의 구성이 제대로 구현될 것으로 인식하리라고는 보이지 아니한다. 이는 반응 중 Vrods의 실측이 어렵다거나 불가능하다 하더라도 마찬가지라 할 것인바, 만약 이 사건 제1항 발명이 반응 중 Vrods 실측치의 획득이 곤란한 사정으로 인해 Vrods 추정치의 사용을 허용하여야 하는 경우에 해당한다고 한다면, 이 사건 명세서에서는 앞서 본 이 사건 제1항 발명의 특성을 고려하여 그와 같은 추정치의 사용이 허용됨을 명시적으로 개시하였어야 한다.
(라) 더구나 Vrods의 추정치는 그 계산 방법에 따라서도 모두 달라질 수 있다 할 것인데, 원고의 주장에 의하더라도 Vrods 추정치의 계산 방법으로 (i) 관측 창을 통하여 반응 중 실리콘 봉의 지름을 직접 측정하여 부피를 계산하는 방법, (ii) 관측 창을 통하여 반응 중 실리콘 봉 사이의 거리를 측정하여 실리콘 봉의 지름 및 부피를 계산하는 방법, (iii) 반응 시간에 따른 실리콘 봉 지름의 선형적 변화를 이용해 최종 생산된 실리콘 봉의 직경 측정으로부터 반응 중 실리콘 봉의 지름 및 부피를 계산하는 방법, (iv) 전류의 양과 실리콘 봉의 지름과의 상관관계를 나타내는 그래프를 얻은 후 전류의 양으로부터 반응 중 실리콘 봉의 지름 및 부피를 계산하는 방법, (v) 반응기의 가스 배출구에 배기가스의 조성을 분석할 수 있는 가스 크로마토그래프를 설치하여 실시간으로 생성된 실리콘 중량을 알아내고, 위 중량을 실리콘 밀도로 나누어 실리콘 부피를 계산하는 방법 등 다양한 방법이 존재하고, 위 추정 계산 방법들이 모두 동일한 부피 추정값을 갖는다고 볼 합리적 근거는 찾아보기 어렵다[특히 (v) 방법의 경우, ‘봉’에 증착된 실리콘 중량에 더하여 ‘브릿지’에 증착된 실리콘 중량까지 포함된 전체 실리콘 중량이 측정되고, 그로부터 Vrods 값이 계산되는 것이므로, 나머지 (i) 내지 (iv) 방법을 통해 계산되는 Vrods의 추정치들과는 당연히 상이한 값이 나올 것으로 예상된다].
사정이 이러하다면, 가사 통상의 기술자가 이 사건 제1항 발명의 Vrods 값에 실측치가 아닌 추정치를 적용하는 시도를 해볼 수 있다 하더라도, 이 사건 제1항 발명의 실시를 위해 위와 같이 불명료하고 다양한 값의 추정치 중 하나를 적용한 통상의 기술자는 자신이 실시하는 발명이 이 사건 제1항 발명의 구성을 제대로 구현한 것인지를 확인할 수 없다 할 것이고(이 사건 명세서상 이 사건 제1항 발명의 효과 대부분이 구체적인 실험, 실시예 등으로 증명되어 있지 아니하고 주8) , 이 사건 제1항 발명의 구성으로 인한 작동원리가 개시되어 있지도 아니함은 후술하는 바와 같은바, 이 사건 제1항 발명의 효과가 얻어지는지 여부를 확인함으로써 이 사건 제1항 발명의 구성이 제대로 구현되었는지를 알아보는 것도 통상의 기술자에게 여의치 않을 것으로 보인다), 이는 이 사건 제1항 발명의 다른 공정변수들인 벽의 온도(Twall), 체적 유량(Q) 역시 후술하는 바와 같이 불명료함을 고려하여 볼 때 더욱 그러하다.
(마) 이와 관련하여 원고는, 갑 제22호증의 기재를 들어 브릿지의 부피가 봉의 부피에 비하여 무시할 만하다는 것이 이 기술 분야의 통상의 기술 상식이어서 봉의 부피에 브릿지의 부피를 포함하여도 이 사건 아르키메데스 수의 값은 유의미하게 변하지 않는다고도 주장하는바, 이는 Vrods 값에 어느 정도의 오차가 있어도 Vrods 값의 의미를 객관적으로 이해하고 이 사건 제1항 발명을 실시하는 것에는 영향이 없다는 취지의 주장인 것으로 보인다.
그러나 갑 제22호증의 기재 내용이, 실리콘 로드의 표면적 계측 방법에, 관측 창을 통해 실리콘 로드의 직경을 직접 측정하는 방법과 가스 크로마토그래프의 조성 분석을 통하는 방법이 있다는 내용임은 앞서 본 바와 같고, 이는 단순히 실리콘 봉의 표면적 측정 방법으로 여러 방법들이 있음을 소개한 것에 불과할 뿐, 위 기재 내용만으로 ‘브릿지의 부피가 봉의 부피에 비해 무시할 만하다’는 점이 인정된다고 볼 수 없다.
또한 브릿지의 부피가 무시될 수 있는지 여부는 그와 같은 판단이 요구되는 지점이 어디인지에 따라 상이하다 할 것인데, ① 앞서 본 바와 같이 구성요소 4의 Vrods는 반응 중 상호 연동된 실제 조절이 중시되는 공정변수 중 하나라는 점, ② 아래에 기재된 (i) 종전 관련 공지기술에 대한 설명으로 보이는 이 사건 명세서상 기재내용 및 (ii) 원고 스스로 밝힌 이 사건 제1항 발명의 도출 경위에서 알 수 있는 바와 같이 반응 중 상호 연동된 공정변수들을 조절하여 반응기 내 유동 조건을 결정함에 있어, 어느 공정변수의 어느 만큼의 변화가 반응기 내 유동 조건을 어느 정도 유의미하게 변화시키는지의 여부는 수많은 실험을 통해서 결정될 수 있을 뿐, 구성요소 4의 Vrods와 브릿지 부피의 단순 수치 비교 만에 의해 일의적으로 판단될 수 있는 것으로 보이지 아니하는 점, ③ 나아가 수많은 실험을 거쳐 이 사건 아르키메데스 수의 수치범위가 결정되었다고 하더라도, 그에 포함된 공정변수인 Vrods에서 브릿지의 부피가 무시될 수 있는지 여부를 밝히기 위해서는 관련 공정변수 7개 모두와 관련한 각각의 연동 관계를 살피는 수많은 경우의 수에 해당하는 실험들 역시 선행되어야 할 것으로 보이는 점 등에 비추어 보면, 구체적 근거를 밝히지 아니한 채 단순히 이 사건 아르키메데스 수의 값이 브릿지 부피의 포함 여부에 불구하고 유의미하게 변하지 않는다는 취지의 원고 주장은 받아들이기 곤란하다.
| (i) 이 사건 명세서 기재내용(식별번호 [0062]) |
| 다결정 실리콘의 증착을 위한 지멘스 반응기에 대해서는 아르키메데스 수와 관련하여 아직 아무런 평가가 이루어져 있지 않다. |
| (ii) 이 사건 제1항 발명의 도출 경위(원고의 2019. 10. 18.자 준비서면 제1 내지 4쪽 참조)〉 |
| 이 사건 제1항 발명의 발명자들은 지멘스 반응기 내의 반응가스 유동이 지멘스 공정에 큰 영향이 있다는 사실을 발견하고, 강제 대류와 자유 대류가 공존하는 공간에서 유체의 유동 조건을 나타낼 수 있는 아르키메데스 수를 도입하는 아이디어를 착안하게 되었다. 지멘스 공정에 아르키메데스 수를 도입하기 위하여 먼저 아르키메데스 수가 그라스호프 수와 레이놀즈 수의 제곱의 비라는 전제를 바탕으로 차원 해석의 원리를 적용하여 지멘스 공정에 큰 영향을 미치는 공정변수들 중 그라스호프 수와 레이놀즈 수에 적용할 공정변수들을 선정하였으며, 이후 수많은 실험을 통해 어떠한 세트의 공정변수들이 비에너지 소비와 관련 있는 값을 나타내는지 조사하여 공정변수 세트들과 비에너지 소비와의 관계를 나타내는 그래프를 작성하여 이를 바탕으로 아르키메데스 수의 수식이 비에너지 소비와 일정한 상관관계가 드러나도록 아르키메데스 수식 내의 공정변수들을 조정하여 이 사건 아르키메데스 수를 도출하게 되었고, 이 사건 아르키메데스 수의 수식이 비에너지 소비와의 상관관계를 잘 드러내고 있음을 확인하였다. 또한 반응이 진행됨에 따라 증가하는 실리콘 봉의 부피가 반응 가스의 유동에도 영향을 미친다는 사실에 착안하여, 반응의 진행 정도를 나타내는 무차원 수로서 반응기의 공부피에 대한 봉의 부피의 비인 충전 수준(FL)을 도입하게 되었다. 나아가 공정변수 및 비에너지 소비 감소의 효과를 나타내는 이 사건 아르키메데스 수의 수치 범위를 결정하기 위하여 발명자들이 실험한 수많은 배치(공정변수 세트들)에 대하여 이 사건 아르키메데스 수를 계산하고, 이를 통해 이 사건 아르키메데스 수 대 FL의 그래프들을 그렸으며, FL이 증가함에 따라 일정한 값 이하의 비에너지 소비를 나타내는 배치의 이 사건 아르키메데스 수가 모두 속하도록 이 사건 아르키메데스 수의 상한 및 하한을 설정하였다. |
(바) 나아가 원고의 나머지 ② 내지 ④ 주장(판결서 34쪽)에 관하여 보건대, 이들 주장 역시 이 사건 아르키메데스 수와 함수 관계에 있는 FL을 구성하는 Vrods 값을 적용함에 있어, Vrods의 실측치가 아닌 추정치를 사용하여도 무방하고, 위 ② 내지 ④ 주장과 어긋나는 어느 정도의 오차(② 반응 초기의 실리콘 봉이 직육면체에 가까움으로부터 발생하는 부피 오차, ③ 반응 중 실리콘 봉의 지름인 D가 축방향으로 변할 수 있음에 따른 부피 오차 및 ④ 반응 중 실리콘 봉의 길이가 성장함에 따른 부피 오차)가 발생한다 해도 연산식과 수치로 한정된 이 사건 아르키메데스 수와 FL의 함수관계에 유의미한 변화가 발생하지 않음을 전제로 하고 있다.
그러나 갑 제17 내지 26, 40, 77호증의 각 기재 및 영상만으로는 ‘반응 초기부터 반응이 진행되는 동안’ 실리콘 봉의 모양을 원기둥 모양으로 간주하는 것이 당해 기술 분야에서 통상의 기술 상식이라는 점(② 주장 관련), 실제 반응 중 실리콘 봉의 길이가 유의미하게 성장하지 않는 점(④ 주장 관련)을 인정하기에 부족하고, 달리 원고의 위 주장들을 인정할 증거도 없다. 오히려 반응 중 각 공정변수가 상호 연동됨이 불가결하여 실제 조절이 중시되는 이 사건 제1항 발명의 특성상 Vrods를 반응 중 실측치가 아닌 추정치로 적용하는 것이 이 사건 명세서상 그러한 취지의 기재 없이도 통상의 기술자에게 자명한 사항이라 할 수 없고, 설령 추정치 사용이 가능하다 하더라도 사용되는 계산 방법에 따라 Vrods의 추정치가 상이해질 수 있으며, 발생된 공정변수의 오차를 이 사건 제1항 발명에서 무시할 만한 것이라고 쉽사리 단정할 수 없음은 앞서 본 바와 같다(② 내지 ④ 주장 관련).
(사) 결국 원고의 위 주장들은 모두 이유 없다.
(3) 따라서 구성요소 4의 공정변수 Vrods는 이 사건 명세서의 발명의 상세한 설명에 그 측정 방법이 기재되어 있지 않고, 통상의 기술자가 출원 시의 기술 수준으로 보아 과도한 실험이나 특수한 지식을 부가하지 않고서는 Vrods를 측정할 수 없으므로, 이를 공정변수로 포함하는 이 사건 제1항 발명의 구성은 그 정확한 이해와 재현이 불가능하다(이에 반하는 갑 제31호증의 기재 및 증인 소외인의 증언은 믿지 아니한다).
다) 구성요소 5(이 사건 아르키메데스 수)에 포함된 벽의 온도(Twall)
(1) 이 사건 명세서에서 이 사건 아르키메데스 수는 ‘Ar = Π * g * L³ * Ad * (Trod - Twall) / (2 * Q² * (Trod + Twall))’로 정의되어 있는데, 여기에 포함된 공정변수 Twall은 ‘벽의 온도’라고 정의되어 있다(식별번호 [0071]). 한편 이 사건 명세서에 ‘실리콘의 증착에 사용되는 지멘스 반응기는 소정의 부피(공부피)를 가진 용기로서 간주될 수 있는데, 상기 부피는 특정 온도 Twall를 가진 벽에 의해 한정된다. 또한 이 공간은 실리콘의 증착 결과 시간이 경과함에 따라 성장하며 특정 온도 Trod를 가진 봉을 수납한다(식별번호 [0063])’고 기재되어 있고, 관련 침해소송의 피고 측 감정인의 보고서(갑 제35호증)에 ‘CVD 반응기 내벽의 온도는 측정 위치에 따라 다양한 값을 가질 수 있으므로, 자연대류에 영향을 끼치는 Twall은 다양한 값을 가지는 내벽 온도 분포를 대표하는 값, 즉 평균 온도라고 생각된다’고 기재되어 있는바, 이를 종합하여 보면, 위 Twall, 즉 벽의 온도는 실리콘 봉이 수납된 공간을 한정하는 ‘반응기 내벽의 평균 온도’를 의미하는 것으로 보인다. 그런데 이 사건 명세서에는 위와 같은 Twall의 측정 방법에 대해 별다른 기재가 없다.
(2) (가) 이에 대하여 원고는, 통상의 기술자라면 이 사건 명세서상 Twall의 측정 방법이 기재되어 있지 않더라도 당해 기술 분야에서 잘 알려진 열전달 이론을 바탕으로 한 아래에 기재된 계산식들 중 하나를 이용하고, 해당 각 계산식에 필요한 ho 주9) (‘냉매의 필름 계수’, ‘대류 열전달 계수’ 또는 ‘열전달 계수’라고도 한다)가 시스템에 적합한 것이 되도록 선정하여 식에 대입한 후 반응기 벽면을 흐르는 냉각수의 각 출입 온도를 적용시킴으로써 반응기 내벽의 온도를 구할 수 있으며, 실제 공정에 있어서도 위와 같은 방법으로 반응 중 Twall의 측정이 이루어지고 있다고 주장한다.

(나) 살피건대, 갑 제61, 64, 86 내지 90호증의 각 기재에 의하면, 학부 수준의 열전달 교과서 주10) 에 전체 평판 상의 흐름이 층류인 경우 열전달 계수를 구할 수 있는 무차원 수인 너셀(Nusselt, 이하 ‘Nu’라 한다) 수가 개시되어 있는 사실, 관련 기술 문헌 주11) 에 ‘통상적인 쟈켓의 흐름은 층류, 층류 및 난류의 중간 또는 난류일 수 있다. (중략) 난류에 대하여 (1)에서 주어진 공식이 평행 평판에 대하여 보정된 최고차 계수와 함께 사용되어 왔다. [ 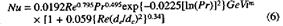 ]’, ‘코일 및 칸막이가 있는 쟈켓 내부 나선형 코일, 하프 파이프 코일 및 나선-칸막이 통상적인 쟈켓에 대하여 하기 (1)식의 식 8이 난류 영역의 흐름에 대하여 직접 적용된다(모든 실용적인 적용 사례에서 흐름은 난류이다.) 도입 보정은 이 식에서 무시된다. [
]’, ‘코일 및 칸막이가 있는 쟈켓 내부 나선형 코일, 하프 파이프 코일 및 나선-칸막이 통상적인 쟈켓에 대하여 하기 (1)식의 식 8이 난류 영역의 흐름에 대하여 직접 적용된다(모든 실용적인 적용 사례에서 흐름은 난류이다.) 도입 보정은 이 식에서 무시된다. [ 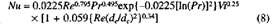 ]’라고 기재되어 있는 사실, 피고가 실제 지멘스 반응기를 운용함에 있어 안전상의 이유로 지멘스 반응기 상부의 온도가 너무 높아지지 않도록 반응기 상부의 대략적인 온도를 측정하고 있는 사실, Twall의 측정 방법이 명세서상 개시되지 아니한 지멘스 공정 기술 분야 관련 특허명세서들에서 ‘냉매의 운전 조건을 조절하기 위하여 폴리실리콘 생산 중 금 층을 약 200 내지 300℃ 범위의 최대 온도에서 유지하여야 한다’(갑 제64호증), ‘상기 반응로의 노 내측 표면 온도를 400℃ 이하로 제어하면서 다결정 실리콘 제조를 하는 것’, ‘반응로의 내벽면을 370℃ 이하로 유지하면서’, ‘열수 출구단 측의 표면 온도는 최고 231℃로 산정되었다’(이상 갑 제88호증), ‘반응로의 내벽의 온도를 250℃, 300℃, 400℃로 유지하여’(갑 제89호증), ‘450℃ 이하의 반응기 벽 온도를 유지하기 위하여 설계되었다’(갑 제90호증)는 등의 기재가 포함되어 있는 사실은 인정된다.
]’라고 기재되어 있는 사실, 피고가 실제 지멘스 반응기를 운용함에 있어 안전상의 이유로 지멘스 반응기 상부의 온도가 너무 높아지지 않도록 반응기 상부의 대략적인 온도를 측정하고 있는 사실, Twall의 측정 방법이 명세서상 개시되지 아니한 지멘스 공정 기술 분야 관련 특허명세서들에서 ‘냉매의 운전 조건을 조절하기 위하여 폴리실리콘 생산 중 금 층을 약 200 내지 300℃ 범위의 최대 온도에서 유지하여야 한다’(갑 제64호증), ‘상기 반응로의 노 내측 표면 온도를 400℃ 이하로 제어하면서 다결정 실리콘 제조를 하는 것’, ‘반응로의 내벽면을 370℃ 이하로 유지하면서’, ‘열수 출구단 측의 표면 온도는 최고 231℃로 산정되었다’(이상 갑 제88호증), ‘반응로의 내벽의 온도를 250℃, 300℃, 400℃로 유지하여’(갑 제89호증), ‘450℃ 이하의 반응기 벽 온도를 유지하기 위하여 설계되었다’(갑 제90호증)는 등의 기재가 포함되어 있는 사실은 인정된다.
(다) 그러나 원고의 이 부분 주장은 모두 구성요소 5의 Twall 값에 열전달 이론을 통해 계산되는 추정값을 적용할 수 있음을 전제로 하고 있다 할 것인데, 이 사건 제1항 발명에서 요구되는 Twall은 전체 공정 기간에 걸쳐 다른 6개 공정변수와 상호 연동 작용을 일으키면서 이 사건 아르키메데스 수와 FL의 함수관계가 특정 연산식 및 수치범위 내로 조절되어야 하는 정도에 부합되는 정확함을 가지고 있어야 함은 앞선 인정사실[위 나) (2) (다)항 이 사건 제1항 발명의 특성 부분 기재 참조]에 비추어 명확한바, 이 경우 통상의 기술자가 이 사건 제1항 발명인 제조방법을 실제 사용함에 있어 Twall을 반응 중 실측치가 아닌 추정치로 적용하더라도 이 사건 제1항 발명의 구성을 제대로 구현한 것이라고 인식하리라고는 보이지 아니하고, Twall의 반응 중 실측이 어렵다거나 불가능하다는 사정이 있다고 하여 달리 볼 것도 아니다. 만약 이 사건 제1항 발명이 Twall의 반응 중 실측치 획득이 곤란한 사정으로 인해 Twall 추정치의 사용을 허용하여야 하는 경우에 해당한다고 한다면, 이 사건 명세서에서는 앞서 본 이 사건 제1항 발명의 특성을 고려하여 그와 같은 추정치의 사용이 허용됨을 명시적으로 개시하였어야 한다.
(라) 나아가 가사 원고 주장의 위 추정 계산식들이 Twall의 측정을 위해 이용될 수 있다고 하더라도, 위 계산식들을 통해 Twall 값을 계산하기 위해서는 모두 구체적인 특정 ho 값(냉매의 필름 계수)을 알고 있어야 한다[위 우측 식의 U= 1/(dw/k + I/ho)](갑 제36호증, 을 제20호증).
이때 위 ho 값은 일반적으로 Nu 수에 관한 식( 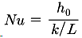 )을 이용하여 구하게 되는데, 위 Nu 수의 값은 유체의 층류, 난류 여부 및 그 정도, 유체가 평판에 따라 흐르는지 아니면 관 내부에 흐르는지 여부, 유체의 물성(점도, 밀도, 비열 등)이 어떤지 등에 따라 이를 구하는 식이 모두 다르다 할 것인바(갑 제43호증, 을 제27호증), 다양한 유체 흐름이 존재하는 시스템에 부합하는 Nu 수를 찾는 것은 앞서 본 학부 수준의 열전달 교과서에 포함된 전체 평판 상의 흐름이 층류인 경우의 너셀수를 찾는 것과는 그 어려움의 정도가 확연히 다르다고 볼 수밖에 없다. 나아가 앞선 관련 기술문헌에 ‘통상적인 쟈켓 흐름이 난류인 경우, 코일 및 칸막이가 있는 쟈켓 내부 나선형 코일의 흐름이 난류인 경우에 해당하는 각 Nu 수’ 주12) 가 개시되어 있다고 하더라도, 이 사건 제1항 발명이 적용될 지멘스 반응기에 대한 봉, 노즐 등의 내부 구조, 반응기의 형태 및 규모가 특별히 한정되어 있지 아니한 이상 해당 각 지멘스 반응기 내 유체 흐름의 경향은 제각기 상이할 수밖에 없으므로, 위와 같이 상이한 각 반응기 시스템의 유체 흐름 경향에 정확히 부합하는 Nu 수를 찾아내는 것이 통상의 기술자에게 용이하다고 볼 수 없다[이는 관련 침해소송의 원고 측 감정인 역시 ho 값 계산을 위한 Nu 수에 관한 식의 적용을 한차례 변경한 적이 있고(갑 제31호증의 8, 9쪽, 을 제20호증의 3, 4쪽 참조), 그와 같이 변경된 식 조차도 원고 스스로 지멘스 반응기와 같거나 유사한 구조의 반응기에 적용되는 Nu 수라고 밝힌 바 있는 주13) ‘통상적인 쟈켓 흐름이 난류인 경우, 코일 및 칸막이가 있는 쟈켓 내부 나선형 코일의 흐름이 난류인 경우에 해당하는 각 Nu 수’에 관한 식과 상이한 점에 비추어 볼 때 더욱 명확하다].
)을 이용하여 구하게 되는데, 위 Nu 수의 값은 유체의 층류, 난류 여부 및 그 정도, 유체가 평판에 따라 흐르는지 아니면 관 내부에 흐르는지 여부, 유체의 물성(점도, 밀도, 비열 등)이 어떤지 등에 따라 이를 구하는 식이 모두 다르다 할 것인바(갑 제43호증, 을 제27호증), 다양한 유체 흐름이 존재하는 시스템에 부합하는 Nu 수를 찾는 것은 앞서 본 학부 수준의 열전달 교과서에 포함된 전체 평판 상의 흐름이 층류인 경우의 너셀수를 찾는 것과는 그 어려움의 정도가 확연히 다르다고 볼 수밖에 없다. 나아가 앞선 관련 기술문헌에 ‘통상적인 쟈켓 흐름이 난류인 경우, 코일 및 칸막이가 있는 쟈켓 내부 나선형 코일의 흐름이 난류인 경우에 해당하는 각 Nu 수’ 주12) 가 개시되어 있다고 하더라도, 이 사건 제1항 발명이 적용될 지멘스 반응기에 대한 봉, 노즐 등의 내부 구조, 반응기의 형태 및 규모가 특별히 한정되어 있지 아니한 이상 해당 각 지멘스 반응기 내 유체 흐름의 경향은 제각기 상이할 수밖에 없으므로, 위와 같이 상이한 각 반응기 시스템의 유체 흐름 경향에 정확히 부합하는 Nu 수를 찾아내는 것이 통상의 기술자에게 용이하다고 볼 수 없다[이는 관련 침해소송의 원고 측 감정인 역시 ho 값 계산을 위한 Nu 수에 관한 식의 적용을 한차례 변경한 적이 있고(갑 제31호증의 8, 9쪽, 을 제20호증의 3, 4쪽 참조), 그와 같이 변경된 식 조차도 원고 스스로 지멘스 반응기와 같거나 유사한 구조의 반응기에 적용되는 Nu 수라고 밝힌 바 있는 주13) ‘통상적인 쟈켓 흐름이 난류인 경우, 코일 및 칸막이가 있는 쟈켓 내부 나선형 코일의 흐름이 난류인 경우에 해당하는 각 Nu 수’에 관한 식과 상이한 점에 비추어 볼 때 더욱 명확하다].
(마) 다른 한편으로, 만약 비슷한 정도의 유체 흐름 경향에 부합하는 Nu 수 및 이에 따른 ho를 찾아 반응기의 Twall를 계산하더라도 이 사건 아르키메데스 수의 산정에 문제가 없는 것이라면, 앞서 본 이 사건 제1항 발명의 특성을 고려하여 볼 때 이 사건 명세서에서는 통상의 기술자에 의해 그와 같은 Twall 측정방법이 사용될 수 있도록 관련 설명을 반드시 개시하고 있어야 한다고 봄이 옳고, 그와 같은 개시가 없는 이상 통상의 기술자는 Twall 측정에 필요한 ho를 찾아내기 위해 과도한 실험이나 특수한 지식을 부가할 수밖에 없다.
(바) 따라서 원고의 위 주장은 어느 모로 보나 이유 없다.
(3) 따라서 구성요소 5의 공정변수 Twall은 이 사건 명세서의 발명의 상세한 설명에 그 측정방법이 명시적으로 기재되어 있지 않고, 통상의 기술자가 출원 시의 기술 수준으로 보아 과도한 실험이나 특수한 지식을 부가하지 않고서는 Twall의 측정 방식을 알 수 없으므로, 이를 공정변수로 포함하는 이 사건 제1항 발명의 구성은 그 정확한 이해와 재현이 불가능하다(이에 반하는 갑 제31호증의 기재 및 증인 소외인의 증언은 믿지 아니한다).
라) 구성요소 5(이 사건 아르키메데스 수)에 포함된 체적 유량(Q)
(1) 이 사건 명세서에서 이 사건 아르키메데스 수에 포함된 공정변수 Q는 ‘작동 조건(p, t) 하에서 개스의 체적 유량(volume flow)’라고 정의되어 있기는 하나(식별번호 [0071]), 그 측정 위치 및 방법에 대하여는 별다른 기재가 없다. 일반적으로 Q는 가스의 부피로서 온도 및 압력에 따라 그 값이 현저하게 달라짐이 기술 상식에 해당하므로(다툼 없는 사실), 위와 같이 측정 위치 및 방법이 특정되지 아니한 구성요소 5의 Q는 통상의 기술자가 이를 용이하게 이해하고 재현할 수 없다.
(2) (가) 이에 대하여 원고는, 통상의 기술자라면 이 사건 명세서상 Q의 측정 위치나 측정 방법에 관한 내용이 기재되어 있지 않더라도 ① 이 사건 아르키메데스 수가 반응기 내부 유체의 전체적인 유동 조건을 설명하는 무차원 수이고, Q는 이러한 이 사건 아르키메데스 수를 구성하는 공정변수인 점, ② 이 사건 명세서에서 ‘유입되는 반응 가스가 강제 대류를 야기한다’고 기재되어 있고, 이 사건 아르키메데스 수의 공정변수들 중에서 반응 가스의 유입 유량과 관련된 것은 오직 Q와, 모든 노즐의 단면적의 합인 Ad 뿐인 점, ③ 강제 대류를 야기하는 유체의 속도가 유입구의 단면적에 큰 영향을 받기 때문에, 유입구를 갖는 닫힌 공간의 시스템에서 강제 대류와 관련된 유체의 유입 속도는 닫힌 공간 내부로 유입되기 직전의 지점에서 측정되어야 함이 통상의 기술 상식인 점 등을 감안함으로써, 구성요소 5의 Q를 ‘노즐(Ad)을 통과하기 직전 반응 가스가 유입되는 위치에서 측정되는 체적 유량’으로 이해하는 동시에 이 사건 명세서상 Q의 정의를 위해 규정된 ‘작동 조건(P, T)’ 역시 Q 값이 관련된 지점, 즉 ‘노즐(Ad)을 통과하기 직전에서의 작동 조건(P, T)’으로 이해할 것임이 명확하다고 주장한다 주14) .
(나) 그러나 ① 원고 주장과 같은 사정, 즉 이 사건 아르키메데스 수가 반응기 내부 유체의 전체적인 유동 조건을 설명하는 무차원 수이고, Q가 이러한 이 사건 아르키메데스 수를 구성하는 공정변수라는 사정이, 통상의 기술자가 출원 시의 기술 수준으로 보아 ‘노즐을 통과하기 직전 반응 가스가 유입되는 위치, 즉 지멘스 반응기의 닫힌 공간 내부로 유입되기 직전에서 측정되는 체적 유량’이 지멘스 반응기 내부 유체의 전체적인 유동 조건을 설명하는 무차원 수인 이 사건 아르키메데스 수를 구성하는 공정변수로 기능함을 인식할 수 있었다는 근거가 될 수 없다. 이는 이 사건 제1항 발명 이전(이전)은 이 사건 명세서에 기재되어 있는 바와 같이 ‘다결정 실리콘의 증착을 위한 지멘스 반응기에 대해서는 아르키메데스 수 주15) 와 관련하여 아직 아무런 평가가 이루어져 있지 않’은 상태였고(식별번호 [0062]), 원고 스스로도 이 사건 제1항 발명의 의미 자체가 ‘여러 실험을 통하여 필라멘트 봉의 길이(L), 모든 노즐의 단면적의 합(Ad), 실리콘 봉의 온도(Trod), 반응기 내벽의 온도(Twall) 및 유입 반응 가스의 총 실제 체적 유량(Q) 등이 지멘스 반응기 내부의 유체 유동에 큰 영향을 미친다는 것을 발견하고, 상기 공정변수들을 차원 해석의 물리적 변수로 선정하여 이 사건 제1항 발명의 파라미터인 이 사건 아르키메데스 수를 도출한 것’ 주16) 이라고 밝히고 있는 점에 비추어 볼 때, 통상의 기술자가 출원 시의 기술 수준으로 보아 이 사건 아르키메데스 수를 구성하는 공정변수들 중 하나인 Q가 명시적인 설명 없이 당연히 ‘노즐을 통과하기 직전 반응 가스가 유입되는 위치, 즉 지멘스 반응기의 닫힌 공간 내부로 유입되기 직전에서 측정되는 체적 유량’으로서 지멘스 반응기 내부 유체의 전체적인 유동 조건을 설명하는 무차원 수인 이 사건 아르키메데스 수를 구성하는 공정변수가 됨을 인식할 수 있다고 볼 수는 없기 때문이다.
(다) 또한 ② 이 사건 명세서에서 ‘유입되는 반응 가스가 강제 대류를 야기한다(식별번호 [0065])’고 기재되어 있다 하더라도, 반응기 내 강제 대류를 야기하는 원인이 되는 ‘유입되는 반응 가스’와, 이로 인해 발생되는 반응기 내 유동 조건을 설명하는 이 사건 아르키메데스 수 및 이를 구성하는 공정변수(Q)는 그 자체로 각각 ‘원인’과 ‘결과’에 해당하는 현상에 관련된 것일 뿐 서로 동일한 것이라 볼 수 없다. 그리고 원고 주장과 같이 이 사건 아르키메데스 수의 공정변수들 중 ‘반응 가스의 유입 유량’과 관련된 것이 오직 Q와 Ad뿐이라 하더라도, 이 사건 아르키메데스 수가 반응기 내부로 가스가 유입되는 결과 발생하는 ‘반응기 내 유동 조건’을 설명하는 무차원 수이고, 통상의 기술자가 ‘강제 대류와 자연 대류가 공존하는 닫힌 공간인 반응기 내 유동 조건을 설명하는 공정변수’에 ‘지멘스 반응기의 닫힌 공간 내부로 유입되기 직전에서 측정되는 체적 유량’이 포함된다고 인식하기 어렵다는 점은 앞서 본 바와 같은바, ‘반응 가스의 유입 유량’ 또는 ‘지멘스 반응기의 닫힌 공간 내부로 유입되기 직전에서 측정되는 체적 유량’이 반드시 이 사건 아르키메데스 수의 공정변수에 포함되어야 함을 전제로 하는 원고의 이 부분 주장은 받아들일 수 없다. 오히려 이 사건 아르키메데스 수가 반응기 내부 의 유동 조건을 설명하는 무차원 수인 점을 감안하면, 이 사건 아르키메데스 수를 구성하는 공정변수인 구성요소 5의 Q는 반응기 내부 의 작동 조건(P, T)에서 측정되는 체적 유량이라고 봄이 보다 상식적인 이해에 해당한다고 볼 여지가 있을 뿐이고, 이는 실제 반응기 내부의 체적 유량 측정이 어렵다거나, 이 사건 제1항 발명과 무관한 통상적인 지멘스 반응 중에 반응 가스의 체적 유량이 반응기 외부, 즉 노즐에 가까운 위치에서 측정되는 경우가 많다 하더라도 마찬가지이다.
(라) 나아가 ③ 강제 대류를 야기하는 유체의 속도가 유입구의 단면적에 큰 영향을 받기 때문에, 유입구를 갖는 닫힌 공간의 시스템에서 강제 대류와 관련된 유체의 유입 속도가 ‘닫힌 공간 내부로 유입되기 직전의 지점’에서 측정되어야 함이 통상의 기술 상식이라는 주장에 관하여 보건대, 우선 원고가 그 주장의 근거로 삼은 갑 제66호증은 이 사건 제1항 발명의 출원일 이후인 2018. 9.경 발행된 논문이므로, 이 사건 제1항 발명 출원 시 통상의 기술자의 인식 정도를 증명하는 자료로 보기는 어렵다. 또한 원고의 주장과 같이 ‘강제 대류를 야기하는 유체의 속도가 유입구의 단면적에 큰 영향을 받는 다’ 하더라도, 그와 같은 사정은 이 사건 아르키메데스 수를 구성하는 공정변수인 구성요소 5의 Q가 어느 위치에서 측정되는 체적 유량을 의미하는 지에 대한 해석 문제와는 별다른 관련이 없는바, 이는 앞서 (나), (다)항에서 살펴본 이유와 같다.
(마) 따라서 원고의 위 주장은 모두 이유 없다.
(3) 따라서 구성요소 5의 공정변수 Q는 이 사건 명세서의 발명의 상세한 설명에 그 측정 위치 및 방법이 명시적으로 기재되어 있지 않고, 통상의 기술자가 출원 시의 기술 수준으로 보아 과도한 실험이나 특수한 지식을 부가하지 않고서는 Q의 의미를 객관적으로 파악하여 측정할 수 없으므로, 이를 공정변수로 포함하는 이 사건 제1항 발명의 구성은 그 정확한 이해와 재현이 불가능하다(이에 반하는 갑 제31호증의 기재 및 증인 소외인의 증언은 믿지 아니한다).
마) 소결
이 사건 명세서에는 구성요소 4, 5의 봉의 부피(Vrod), 벽의 온도(Twall), 체적 유량(Q)의 각 측정 방법이 용이하게 실시될 수 있을 정도로 명확히 기재되어 있지 아니한바, 통상의 기술자는 출원 시의 기술 수준으로 보아 이 사건 명세서의 기재로는 이 사건 제1항 발명의 구성을 용이하게 사용할 수 없다.
2) 이 사건 제1항 발명에 의한 효과를 통상의 기술자가 충분히 예측할 수 있는지 여부(발명의 효과에 대한 이해 및 재현 여부)
가) 명세서 관련 기재 및 쟁점
(1) 이 사건 명세서 기재 내용 중 이 사건 제1항 발명의 효과에 관한 주요 내용은 아래와 같다.
| 배경기술 |
| 【0016】 지멘스 공정을 토대로 하는 폴리실리콘 증착 공정으로서 공지된 모든 방법들은 달성되는 생성물의 품질이 좋지 않으며, 제조 공정의 경제성이 떨어진다. |
| 【0017】 생성물의 품질에 관한 단점은 특히 봉의 직경에 있어서 축방향으로 변동이 관찰되는 경우가 흔하며, 어떤 경우에는 봉의 표면 특성이 불량하다. |
| 【0018】 상기 공정들은 상승된 수준의 에너지를 필요로 하는 경우가 흔하다. |
| 【0019~0021】 어떤 경우에는 봉이 반응기 안에서 넘어지고, 일부 공정에서는 실리콘 분진이 형성되거나, 과열이 일어나고, 최악의 경우 실리콘 캐리어 본체(봉 및 브릿지)의 용융도 발생된다. |
| 【0026】 그러나, EP 2 077 252 A2 및 EP 2 067 744 A2에 개시된 공정들에 의하면 반응기에서 넘어지는 봉의 수가 증가되는 것으로 나타났다. 이는 아마도 반응 개스의 유입 속도의 갑작스러운 변화와 관련이 있는 것으로 보인다. |
| 【0027】 사용되는 얇은 봉의 길이는 수 미터(통상 2-3 m)일 수 있다. 봉이 넘어지는 경우, 인접하는 다른 봉을 건드릴 수도 있다. |
| 【0028】 이는 상당한 경제적인 손실을 야기하며, 이런 식으로 오염된 실리콘 봉을 복잡한 방식으로 세정해야 하는 경우에 특히 그러하고, 봉이 넘어질 때 반응기가 손상되는 경우에는 더욱 그러하다. |
| 【0029】 증착 공정이 완료되기 전에 이러한 경우가 발생하면, 넘어진 봉을 복구하기 위해 증착 공정을 즉시 중단시켜야 한다. 이는 해당 플랜트의 경제성에 직접적인 영향을 미친다. 반응기에 봉이 많이 있을수록 경제적인 손실은 커진다. 한편, 정상적인 작동시에 높은 경제성은 반응기 내 많은 수의 봉과 직접 연관된다. |
| 【0030】 EP 2 067 744 A2에 개시된 공정의 또 다른 단점은, 봉의 전장에 걸쳐 일정한 구조 또는 형태를 달성하는 것과 동시에 충분히 높은 증착 속도를 달성하는 것이 확실히 불가능하다는 것이다. |
| 【0031】 증착 공정 동안 실리콘 봉의 구조는 이상적으로는 커지는 반경의 실린더에 대응한다. 이러한 실린더 형태에서 일탈하면 공정에 혼란이 야기될 수 있다. 가장 좋지 않은 경우에는, 봉들이 함께 융합될 수 있고 증착 공정이 중단될 수 있다. 상기 언급한 일탈의 예를 들면, 형태가 하방으로 좁아지는 원추형인 경우에는 중량의 분포가 불리하게 됨에 따라 봉이 넘어지게 될 위험성이 증가한다. |
| 【0032】 후에 FZ 공정에 사용될 폴리실리콘에 대한 요건이 특히 엄격하다. 사용 전에, 봉을 공칭 직경을 가진 구형으로 분쇄(grinding)해야 한다. 타겟 직경을 조금이라도 초과한다는 것은, 구형 분쇄 과정에서 제거되는 물질의 양이 증가된다는 것이며, 따라서 귀중한 실리콘이 손실된다는 것을 의미한다. 반면, 직경이 타겟 직경보다 작으면, 사용되는 봉의 길이가 감소되므로, 타겟 생성물의 경제성이 악화된다는 것을 의미한다. |
| 【0033】 폴리실리콘 봉은 길이 및 직경 뿐만 아니라 추가적인 파라미터에 의해서도 설명될 수 있다: 봉의 표면의 성질은 다를 수 있다. 봉은 콜리플라워와 같은 표면을 가질 수 있다. 그러나 봉은 또한 거의 평탄한 표면을 가질 수도 있다. 봉의 표면의 전체적인 성질은 이하 "형태(morphology)"라는 용어로 언급될 것이다. |
| 【0034】 기본적으로 높은 평균증착속도(mean deposition rate)는 높은 생산성을 얻기 위해서는 필수적으로 중요하며, 따라서 공정의 경제성을 얻기 위해서도 중요하다. 그러므로, 증착속도를 가능한 한 최대화시키기 위한 노력이 경주되어 왔다. 그러나, 높은 증착속도는 통상적으로 예를 들어 형태에 악영향을 미치는 공정 조건을 필요로 한다. |
| 【0035】 DE 102 007 047 210 A1은 유리한 굽힘 강도(flexural strength)를 가진 폴리실리콘 봉을 만드는 방법을 개시하고 있다. 또한, 이 공정에서 비에너지 소비는 특히 낮다. 공정 기술 관점에서, 클로로실란 혼합물의 유속의 최대값은 30 시간 이내, 바람직하기로는 5시간 이내에 달성되며, 브릿지의 하면의 온도는 1300℃ 내지 1413℃이다. |
| 【0036】 문제는 브릿지의 내부의 온도가 DE 102 007 047 210 A1에 따른 1300℃ 내지 1413℃로 유지되는 브릿지 표면의 온도보다 높을 수 있다는 것이다. |
| 【0037】 온도는 봉과 브릿지에서 전류에 의해 조절된다. 개스 유입에 의한 브릿지 표면의 냉각의 경우에 온도가 유지될 수 있도록 하기 위해서는, 전류가 증가되어야 한다. |
| 【0038】 실리콘과 같은 반도체들은 온도가 높아질수록 전기 저항이 저하되는 성질을 가지고 있는 것으로 알려져 있다. |
| 【0039】 가열된 봉의 내부의 온도가 반응 개스에 의해 냉각되는 그 표면의 온도보다 높기 때문에 봉의 내부와 브릿지의 전기 저항이 낮아진다. 그러므로, 브릿지 내부의 전류는 높아진다. 반응 개스에 의한 브릿지 표면의 극심한 냉각으로 인해 열 유동이 높아지는 제한된 경우에, 브릿지 내부의 온도가 실리콘의 융점(1413℃)보다 높아질 수 있다. 이로 인해 브릿지 누출(bridge leakage)을 초래할 수 있으며, 이는 불가피하게 증착 공정의 중단을 초래한다. |
| 【0040】 DE 10 2007 047 210 A1은 브릿지 누출의 가능성이 크게 증가되는 공정을 개시하고 있다. |
| 【0041】 이것은 브릿지 온도를 저하시키는 것에 의해서만 방지될 수 있지만, 이는 다시 비교적 높은 증착 속도와 개선된 에너지 효율이라는 장점을 무력화시키게 될 것이다. |
| 【0044】 그러나, DE 10 2007 023 041 A1에 따라 제조되는 폴리실리콘 봉은 결정의 길의의 함수로서 직경이 충분히 일정하지는 않은 구조를 나타낸다. 직경은 결정의 길이에 따라 다르며, 이는 기계적인 가공 후 공칭 직경을 얻기 위해서는 한쪽의 물질이 더 많이 제거되어야 하는 결과를 초래한다. 이는 공정의 경제성을 떨어뜨린다. |
| 【0045】 실리콘- 함유 개스가 봉의 표면에 증착되지 않고 (불균일 증착), 그 대신 반응하여 자유 부피의 실리콘을 생성 (균일 증착)하는 경우를 분진 증착(dust deposition)이라고 한다. |
| 【0046】 형성된 분진은 먼저 증착 공정의 종료 시점에서 반응기의 베이스에서 발견되는데, 후속 단계에서 처분되어야 한다. |
| 【0047】 두 번째로, 분진은 방출 개스와 함께 방출 개스 처리부로 이송되어, 문제를 야기할 수 있다. |
| 【0048】 심각한 분진 증착은 증착 공정을 중단시킬 수 있고, 이는 경제성을 떨어뜨린다. |
| 【0049】 또한, 그것은 공업 시설에 상당한 문제를 야기하며, 이와 관련하여 추가의 비용과 불편을 초래한다. |
| 【0050】 불행하게도, 특히 높은 증착 속도를 이용하는 특별한 증착 공정은 일부 경우에 분진 증착을 증가하는 것으로 밝혀지고 있다. |
| 【0051】 결론적으로, 지금까지의 종래 기술로는 폴리실리콘의 증착 공정에서 중요한 여러 가지 측면을 조화시키는 것이 불가능했다. |
| 발명의 내용 |
| 【0052】 본 발명의 목적은 전술한 문제를 해소하기 위한 것이다. |
| 【0058】 상기 공정과 아르키메데스 수에 대한 본 발명의 범위는 반응기의 크기와 관계 없다. 그러므로 상기 공정은 작은 반응기와 큰 반응기 모두에 대해 적절하게 적용된다. |
| 【0059】 마찬가지로, 상기 공정은 반응기에 존재하는, 실리콘이 증착되는 필라멘트 봉의 수 및 길이와는 관계없다. |
| 【0081】 그러나, 본 발명에 따른 공정은 이미 앞서 언급한 바와 같이 반응기 내의 봉의 수와 관계가 없다. |
| 【0082】 (선략) 봉의 수를 두 배로 증가시키는 경우에 최적 공정은 다시 본 발명에 따른 공정에서 청구된 유동 조건에 대응하는 유동 조건을 필요로 한다. |
| 【0083】 아르키메데스 수가, 5%까지의 충전 수준 FL에 대해서는 함수 Ar = 2000 x FL-0.6 에 의한 하한값과 함수 Ar = 17000 x FL-0.9에 의한 상한값으로 정해지는 범위 내이고, 충전 수준 FL이 5% 보다 큰 경우에는 750 내지 4000의 범위 내인 모든 공정의 경우에, 다음과 같은 유리한 기술적인 효과가 동시적으로 및 반복적으로 발생한다. |
| 【0084】 종래 기술과 동일하거나 또는 종래 기술보다 높은 평균 증착 속도에서는 분진 증착이 거의 관찰되지 않는다. |
| 【0085】 본 발명에 따른 공정이 수행될 때, 봉 및/또는 브릿지의 누출이 발생하지 않는다. |
| 【0086】 (선략) 그러므로, 전체 반응기에 대한 최적 유동 조건과 관련하여, 브릿지의 누출이 방지된다. |
| 발명의 효과 |
| 【0087】 본 발명의 방법에 따르면, 넘어지는 봉의 비율은 종래 기술에서 알려진 공정의 경우에 비해 훨씬 낮은 것으로 나타났다. |
| 【0088】 본 발명의 방법에 의해 제조되는 모든 다결정 봉은 종래 기술과 바교하여 봉의 길이에 걸쳐 직경의 편차가 작다. |
| 【0089】 또한, 본 발명에 따른 방법에 있어서, 실리콘 봉의 형태는 봉 상의 축 위치와 무관하고, 증착 설비 내 봉의 위치와도 무관하며, 즉 위치에 관계 없이 모든 봉이 유리한 형태를 가지고 있는 것으로 나타났다. |
| 발명의 실시를 위한 구체적인 내용 |
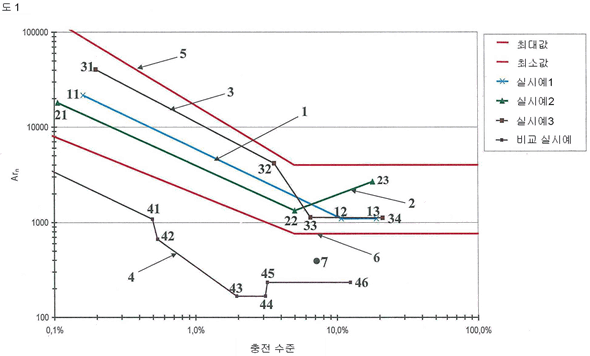
| 【0092】 도 1은 충전 수준의 함수로서 아르키메데스 수의 바람직한 범위를 나타낸다. 곡선이 이중- 로그 형태(double-logarithmic form)로 나타나 있다. |
| 【0093】 본 발명의 범위는 아르키메데스 수의 최대 및 최소 프로파일을 보여주는 라인 5와 6으로 나타나 있다. FL = 5% 까지는, 이들 라인은 지수 함수를 나타낸다. |
| 【0095】 FL = 5% 이하에서 단일 공정에 대한 곡선은 FL 〉 5%의 경우의 아르키메데스 수에 대해 허용되는 범위를 벗어나지 않도록 하는 범위에 있어야 하는 것으로 나타나고 있다. |
| 【0103】 본 발명에서는 아르키메데스 수가 임의의 충전 수준에 대해 곡선 5 및 6에 의해 정해지는 범위를 벗어나지 않아야 한다. |
| 【0104】 본 발명자들은 아르키메데스 수가 전술한 범위를 벗어나는 모든 공정들이 종래 기술에서 이미 알려진 바와 같은 상당한 문제점들과 관련되어 있다는 것을 알게 되었다. |
| 비교실시예 |
| 【0106】 곡선 4는 EP 2 067 744 A2에 의해 공지된 공정에 대한, 충전 수준의 함수로서의 아르키메데스 수를 나타낸다. |
| 【0107】 아르키메데스 수의 측정에 필요하지만 본 출원에 개시되지 않은 모든 파라미터들에 대해서, 전형적인 수치가 추정 또는 계산되었다. 노즐의 면적은 닫힌 노즐의 비율로부터 계산되었다. |
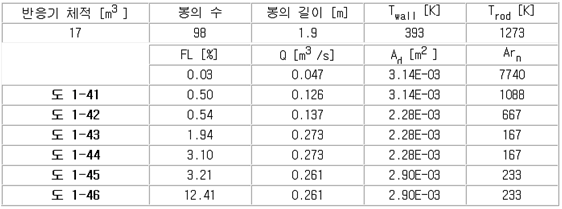
| 【0109】 포인트 41, 42, 43, 44, 45, 및 46은 도 1에 나타나 있다. |
| 【0111】 EP 2 067 744 A2에 개시된 공정에 대한 아르키메데스 수의 그래프는 본 발명의 아르키메데스 수의 범위에 못 미치며 전혀 다른 특성을 보여주고 있는데, 이는 반응 개스의 유입 속도의 변화에 기인하는 것으로 보인다. |
| 【0112】 특히, 넘어지는 봉의 비율이 증가되는 것으로 관찰된다. 증착 속도 역시 균일한 떨어지는 형태가 허용되는 때에만 충분히 높다. 아르키메데스 수의 증가가 이러한 문제들을 제거할 수 있다는 사실이 놀랍다. |
| 【0113】 DE 29 661 A1에 개시된 공정은 또한 충전 수준의 함수로서 아르키메데스 수의 그래프를 보여주고 있는데, 이것은 본 발명의 범위보다 낮다(EP 2 067 744 A2에 개시된 공정과 유사하지만, 구체적인 그래프는 없다). 이 공정에서, 이중- 제트형 노즐이 사용된다. 다음과 같은 파라미터가 사용되었다: |

| 【0115】 포인트 7은 도 1에 나타나 있다. |
| 【0116】 봉의 구조의 균일성과 관련하여 DE 29 12 661 A1에 기재된 장점이 이러한 공정에서 관찰될 수 있지만, 이 공정은 다른 단점들을 상당히 나타낸다. |
| 【0117】 예를 들어, 아르키메데스 수와 관련하여 본 발명의 범위 내에 있는 공정들 보다 비에너지 소비가 훨씬 높다. |
| 【0118】 반면, 본 발명의 공정의 경우 비에너지 소비가 10-20% 낮다. |
| 【0119】 또한, 비교 실시예의 공정에 따르면, 넘어지는 봉의 비율이 뚜렷하게 증가한다. |
| 실시예 |
| 【0122】 본 발명에 따른 3개의 상이한 공정이 제시된다. |
| 【0123】 서로 다른 반응기가 사용되었는데, 이들 반응기는 반응기의 체적 및 봉의 수에 있어서 서로 상이하다. |
| 【0124】 상기 공정들 중 하나의 공정(실시예 1)에 있어서, 48개의 봉과 12.7 m³의 체적을 가진 반응기가 사용되었다. 다른 공정(실시예 2)에서는 체적이 10 m³인 반응기에 들어 있는 24개의 봉에 대해 증착이 수행되었다. |
| 【0125】 세 번째 공정(실시예 3)에서는, 반응기 체적이 5.9 m³에 불과했고, 봉의 수는 마찬가지로 24개였다. |
| 【0126】 모든 공정에서 봉의 길이는 2.9 내지 3.1 m 였다. |
| 【0127】 표 3은 도 1에 도시된 곡선 1의 3개의 포인트 11, 12 및 13의 파라미터들을 나타낸다. |
| 【0128】 벽의 온도 Twall은 393 K로 일정했다. 노즐의 단면적은 4.185 x 10-³㎡로 일정했다. |
| 【0129】 두 번째 컬럼에 반응기의 충전 수준이 나타나 있다. |
| 【0130】 봉의 온도 Trod는 0.16%의 충전 수준에서 1326 K로부터 19%의 충전 수준에서 1302 K로 하강한다. |
| 【0131】 Q는 작동 조건하에서 반응 개스(트리클로로실란 및 수소)의 체적 유량을 나타내며, 그 단위는 m³/s 이다. Q는 처음에는 증가하고 그 후에는 일정하게 유지된다. |
| 【0132】 Arn은 아르키메데스 수를 나타낸다. |
| 【0133】 이 경우에, 아르키메데스 수는 10.76%의 충전 수준과 19.06%의 충전 수준 사이에서 반드시 일정하게 유지된다. 이는 또한 반응 개스의 체적 유량에도 적용되며, 0.192 m³/s로 일정하다. |

| 【0135】 표 4는 도 1에 도시된 곡선 2(실시예 2) 상의 3개의 포인트 21, 22 및 23의 파라미터들을 나타낸다. 이 경우에도 반응기의 벽의 온도 Twall은 393 K로 일정하였다. 노즐의 단면적 역시 일정하게 유지되었고, 이 경우 2.161 x 10-³㎡ 였다. |
| 【0136】 봉의 온도 Trod는 0.106%의 충전 수준에서 1364 K로부터 17.98%의 충전 수준에서 1306 K로 하강한다. 이 경우에 아르키메데스 수는 5.03%의 충전 수준과 17.98%의 충전 수준 사이에서 1332로부터 2671로 높아진다. |

| 【0138】 표 5는 도 1에 도시된 곡선 3(실시예 3) 상의 4개의 포인트 31, 32, 33 및 34의 파라미터들을 나타낸다. 이 경우에도 반응기의 벽의 온도 Twall은 393 K로 일정하였다. 노즐의 단면적 역시 일정하게 유지되었고, 이 경우 8.18 x 10-4㎡ 였다. |
| 【0139】 봉의 온도 Trod는 0.197%의 충전 수준에서 1299 K로부터 21.1%의 충전 수준에서 1233 K로 하강한다. |
| 【0140】 곡선 3(실시예 3)에서, 아르키메데스 수는 3.604%의 충전 수준과 6.5%의 충전 수준 사이에서 낮아졌는데, 충전 수준이 3.604% 보다 낮은 경우의 감소 수준에 비해 더 높은 수준으로 낮아졌다. |
| 【0141】 충전 수준 6.5%로부터 아르키메데스 수의 그래프가 일정하게 유지된다. 이때 반응기의 체적 유량도 0.058 m³/s 로 일정하게 유지된다. |

(2) 통상의 기술자가 이 사건 제1항 발명인 다결정 실리콘의 제조방법으로부터 발휘되는 효과를 이 사건 명세서의 기재를 통해 정확하게 이해하고 재현하기 위해서는, 이 사건 제1항 발명의 각 청구범위 전체에 걸쳐 ① 그와 같은 효과가 이 사건 명세서에서 구체적인 실험, 실시예 등으로 증명되거나, ② 통상의 기술자가 출원 시 기술 수준으로 보아 이를 능히 예측할 수 있어야 한다.
(3) 한편, 이 사건 제1항 발명의 용이 실시 여부와 관련하여 피고는 (i) 이 사건 아르키메데스 수의 유도과정이 위 용이 실시 여부 판단을 위해 이 사건 명세서 기재 등을 통해 밝혀져야 하고, (ii) 출원 이후 원고가 밝힌 이 사건 아르키메데스 수의 유도과정에 과학적·기술적 오류가 있어 통상의 기술자가 이 사건 제1항 발명을 쉽게 실시할 수 없다고 주장하는바 주17) , 이하에서는 먼저 위 (i), (ii) 주장 부분에 관하여 살펴본 후, 앞서 본 이 사건 제1항 발명 효과의 이해 및 재현 여부에 관한 위 ①, ② 부분을 차례로 살펴보기로 한다.
나) 이 사건 아르키메데스 수의 유도과정에 대하여
(1) 피고의 구체적 주장
피고는 ‘이 사건 명세서 기재를 통해서는 이 사건 아르키메데스 수의 기술적 의미를 전혀 이해할 수 없는바, 이 사건 명세서(식별번호 [0054], [0055], [0060] ~ [0062], [0067], [0068])에서 아르키메데스 수의 유도과정에 대해 언급하고 있으므로, 통상의 기술자가 이 사건 아르키메데스 수의 기술적 의미를 명확히 이해하고 이 사건 제1항 발명을 용이하게 실시할 수 있는지 여부를 판단함에 있어 그 유도과정을 참작할 필요가 있다’ 주18) 고 하면서 이 사건 제1항 발명의 용이 실시 여부에 대한 판단을 위해 이 사건 아르키메데스 수의 유도과정이 밝혀져야 한다는 취지로 주장한다.
(2) 판단
우선 피고가 주장하는 이 사건 아르키메데스 수의 ‘기술적 의미’(또는 ‘기술적 의의’ 주19) )는, 피고의 해당 주장 전후의 맥락에 비추어 볼 때 구 특허법 제42조 제3항 제1호 에서 규정한 ‘발명의 상세한 설명’에 대한 기재요건과 관련된 의미로서, 발명의 상세한 설명에서 요구되는 정도로 기재된 당해 발명 구성요소의 내용 및 효과를 나타내는 것으로 보이는바, 그 이해의 자료로서 주장된 이 사건 아르키메데스 수의 유도과정의 개시 여부 역시 그것이 발명의 상세한 설명에서 요구되는 명세서 기재의 정도에 포함되는지 여부에 달려 있다.
한편, 앞선 발명의 상세한 설명 기재불비에 대한 판단 기준(위 3. 가.항 기재 참조)에 비추어 보면, 특허법상 발명의 상세한 설명에 대한 기재는 통상의 기술자가 출원 시의 기술 수준으로 보아 과도한 실험이나 특수한 지식을 부가하지 않고서도 명세서의 기재에 의하여 당해 발명의 구성 및 효과를 정확하게 이해할 수 있고 동시에 재현할 수 있는 정도일 것이 요구되고, 경우에 따라 당해 발명의 내용과 기술 수준에 비추어 예측가능성 내지 실현가능성이 현저히 부족한 발명에 있어서 그 발명의 구성 및 효과를 정확히 이해하고 용이하게 재현하기 위한 명세서 기재의 정도에 개별적 차이가 존재할 수 있을 뿐이므로, 통상의 기술자가 당해 발명의 구성 및 이에 따른 효과를 정확히 이해하고 용이하게 재현할 수 있는 한, 발명에 이르게 된 도출과정 또는 작동원리가 출원 당시 명세서에 기재되어 있지 않다는 사실 자체로 발명의 상세한 설명에 대한 기재불비가 발생하는 것은 아니다. 다만 핵심 구성요소의 유도과정 또는 작동원리가 명세서에 기재되지 않음으로 인하여 통상의 기술자가 명세서상 구체적 실시예에 개시된 범위를 넘어 청구범위에서 한정한 수치범위 전체에 걸쳐 그 발명의 구성에 의한 효과를 명확하게 이해하고 용이하게 재현할 수 없는 경우가 발생할 수 있고, 그로 인해 출원인이 넓은 청구범위를 보호받지 못할 위험성이 발생할 수는 있겠으나, 이는 기본적으로 출원인의 명세서 작성에 대한 선택의 문제로서, 발명에 이르게 된 도출과정 또는 작동원리가 반드시 명세서에 기재되어 있어야 하느냐의 문제와는 별개의 문제이다. 또한 새로운 파라미터를 구성요소로 포함하는 파라미터발명이라 할지라도 발명의 상세한 설명에 대한 기재불비의 판단기준을 특별히 달리 보아야 할 이유는 찾아볼 수 없는바, 위와 같은 판단기준은 파라미터발명에도 그대로 적용될 수 있다.
위 판단 기준에 비추어 이 사건에 돌아와 보건대, 이 사건 제1항 발명의 상세한 설명 기재불비 여부는 이 사건 명세서의 기재 내용 및 출원 시의 기술 수준에 대한 적절한 고찰을 통해 통상의 기술자가 이 사건 제1항 발명의 구성 및 이에 따른 효과를 정확히 이해하고 용이하게 재현할 수 있는지를 판단하는 것으로 족하다 할 것인데, 이 사건 제1항 발명의 구성에 대한 ‘발명의 상세한 설명 기재불비 여부’는 해당 각 구성요소의 의의, 측정 기준 및 방법이 통상의 기술자가 실시 가능한 정도로 기재되어 있는지 여부를 판단함으로써 그 기재불비 여부를 결정하는 것일 뿐 이 사건 아르키메데스 수의 유도과정을 개시하였는지 여부와는 직접적 관련이 없다. 또한 이 사건 제1항 발명의 효과에 대한 ‘발명의 상세한 설명 기재불비 여부’ 역시 이 사건 제1항 발명의 구성에 따른 효과가 이 사건 명세서에서 구체적인 실험, 실시예 등으로 증명되었는지 또는 위와 같은 구체적인 실험, 실시예 등으로 직접 증명되어 있지는 아니하더라도 통상의 기술자의 출원 시 기술 수준으로 능히 예측될 수 있는 정도에 해당하는지를 밝힘으로써 그 기재불비 여부를 결정하는 것이라 할 것인바, 그와 같은 직접 증명 또는 통상의 기술자의 예측가능성 판단에 이 사건 아르키메데스의 유도과정 또는 작동원리가 반드시 필요하다고 볼 근거는 없다[다만 앞서 본 바와 같이 이 사건 제1항 발명의 핵심 구성요소라고 할 이 사건 아르키메데스 수의 유도과정 또는 작동원리가 명세서에 기재되지 않음으로 인하여 통상의 기술자가 이 사건 명세서상 구체적 실시예에 개시된 범위를 넘어 청구범위에서 한정한 수치범위 전체에 걸쳐 그 발명의 구성에 의한 효과를 명확하게 이해하고 용이하게 재현할 수 없는 경우가 발생되는지는 별개의 문제라 할 것으로서, 이에 대하여는 후술하는 ‘이 사건 제1항 발명의 효과가 통상의 기술자의 출원 시 기술 수준으로 능히 예측될 수 있는지 여부’ 항목에서 판단하기로 한다].
나아가 피고가 적시한 이 사건 명세서 기재 부분(식별번호 [0054], [0055], [0060] ~ [0062], [0067], [0068])은 이 사건 아르키메데스 수의 유도과정에 대한 언급이 아니라, 일반적 아르키메데스 수에 대한 설명 또는 지멘스 공정과 아르키메데스 수 사이의 개괄적 관계 설명에 해당하는 부분일 뿐이므로[오히려 이 사건 명세서상 ‘지멘스 반응기에서 봉에 대한 아르키메데스 수의 구체적인 유도 방법에 대해서는 여기서는 다시 설명하지 않기로 한다(식별번호 [0068])’는 기재에 의하면 그 유도과정에 대한 설명이 의도적으로 배제된 것으로 보인다], 특별히 이 사건 아르키메데스 수의 유도과정이 밝혀져야 한다는 피고 주장의 근거가 되는 것으로는 보이지 아니한다.
따라서 피고의 위 주장은 이유 없다.
다) 이 사건 아르키메데스 수에 과학적·기술적 오류가 존재하는지 여부 주20)
(1) 피고의 구체적 주장
(가) 반응기 내 유체의 유동 조건을 지배하여 실리콘 봉을 성장시키는 이 사건 제1항 발명의 특징을 고려할 때 이 사건 아르키메데스 수는 하나의 동일한 반응계인 반응기 내부에서 자유대류와 강제대류가 동시에 이루어지는 유체를 대상으로 하는 것이 기술 상식에 부합한다 할 것인데, 원고가 밝힌 이 사건 아르키메데스 수의 유도과정(이하 ‘이 사건 유도과정’이라 한다)에 의하면 자유대류는 반응기 내부의 유체의 유동을, 강제대류는 노즐에서의 유체의 유동을 각 고려하고 있어 기술 상식에 부합하지 않는다. 나아가 위와 같이 자유대류와 강제대류의 각 대상 유체를 달리 한 결과 이 사건 아르키메데스 수가 도출된 그라스호프 수와 레이놀즈 수에 공히 포함된 각 특성 길이가 달라져 위 유도과정의 분자 및 분모에서 각 소거되지 않게 되는데, 동일한 반응계의 유체를 대상으로 한 이 사건 아르키메데스 수의 그라스호프 수와 레이놀즈 수에 포함된 각 특성 길이는 동일하여 유도과정 중 소거되는 것이 맞으므로, 이와 다른 유도과정에 의한 이 사건 아르키메데스 수는 기술 상식에 부합하지 않는다.
(나) 반응기 내부에서의 반응 가스의 점도 및 밀도와 노즐에서의 원료 가스의 점도 및 밀도가 명백히 다름에도, 이 사건 유도과정에서는 이들 점도 및 밀도가 동일하다고 보아 분자 및 분모에서 각 소거하였는데, 이는 과학적 타당성이 결여된 것이다.
(다) 이 사건 유도과정에서 자유대류의 발생 원인이 되는 부력과 관련된 ΔT를 산정함에 있어 이를 봉의 온도(Trod)와 벽의 온도(Twall)의 차이로 보고 산정하고 있으나, 위와 같은 ΔT의 산정은 가열된 수직 평판의 온도와 잠잠한 구간의 유체의 온도 차이에 의해 자유대류가 발생된다는 통상의 기술 상식에 비추어 타당성이 결여된다.
(라) 원고는 이 사건 유도과정으로 아래와 같이 서로 다른 2가지 유도과정을 제시하였는데, 그 유도과정들의 최종식이 서로 상이한데다가, 유도과정 2의 최종식은 이 사건 아르키메데스 수와 상이하기까지 하므로, 적절한 유도가 이루어졌다고 볼 수 없다.

(마) 유도과정 1의 경우, 반응기 내부에서의 반응 가스의 동적 점성도와 노즐에서의 원료 가스의 동적 점성도가 명백히 서로 다름에도 불구하고 이들 동적 점성도가 동일하다고 보아 분자와 분모에서 각 소거하는 기술적 오류를 범하였다.
(바) 유도과정 2의 경우, (i) 분모의 관성력 식( 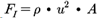 )에서 속도(u)는 노즐에서의 원료 가스의 속도를, 밀도(ρ)는 반응기 내부에서의 반응 가스의 밀도를 적용하여 관성력에 대한 하나의 식에서 서로 다른 반응계의 값을 각각 적용하는 기술적 오류를 범하였고, (ii) 물리적으로 서로 다른 방향의 흐름을 나타내는 음의 부호를 그 유도과정 중 무시하는 오류를 범하였으며, (iii) 그라스호프 수의 관성력(자유대류에서의 관성력)과 레이놀즈 수의 관성력(강제대류에서의 관성력)이 다른 개념이어서 서로 약분될 수 없음에도 불구하고 이를 동일하게 보아 약분하는 오류를 범하였다.
)에서 속도(u)는 노즐에서의 원료 가스의 속도를, 밀도(ρ)는 반응기 내부에서의 반응 가스의 밀도를 적용하여 관성력에 대한 하나의 식에서 서로 다른 반응계의 값을 각각 적용하는 기술적 오류를 범하였고, (ii) 물리적으로 서로 다른 방향의 흐름을 나타내는 음의 부호를 그 유도과정 중 무시하는 오류를 범하였으며, (iii) 그라스호프 수의 관성력(자유대류에서의 관성력)과 레이놀즈 수의 관성력(강제대류에서의 관성력)이 다른 개념이어서 서로 약분될 수 없음에도 불구하고 이를 동일하게 보아 약분하는 오류를 범하였다.
(2) 판단
(가) 갑 제6호증의 1 내지 3의 각 기재에 변론 전체의 취지를 종합하면, 독일 뮌헨 공과대학교 화학공학과(또는 기계공학과) 교수, 독일 화학공학 협의회 부회장 등을 역임한 이 기술분야의 박사학위 소지자들인 요한 슈티클마이어(Johann Stichlmair), 하랄트 클라인(Karald Klein), 세바스티안 레펠트(Sebastian Rehfeldt)에 의해 다음과 같은 내용으로 이 사건 제1항 발명에 대한 평가 진술이 이루어진 사실이 인정된다[원고는 위 증거방법들의 존재를 알지 못한다는 이유로 그 진정성립 여부를 다툰다. 살피건대, 사문서는 진정성립이 증명되어야만 이를 증거로 할 수 있으나 그 증명의 방법에 관하여 특별한 제한이 없고, 당사자가 부지라고 다투는 서증에 관하여 거증자가 특히 그 성립을 증명하지 아니한 경우라 할지라도 법원은 다른 증거에 의하지 아니하고 변론 전체의 취지를 참작하여 자유심증으로 그 성립을 인정할 수 있는데( 대법원 2010. 2. 25. 선고 2007다85980 판결 참조), 원고가 다투고 있는 위 증거방법들의 각 기재 내용, 형식 및 변론 전체의 취지 등에 비추어 보면 위 각 서증은 모두 그 진정성립을 인정할 수 있다].
| ○ 어떠한 시스템에 어느 물리적 양이 적절한 영향력을 갖는지는 대개 기술적인 조사의 결과이고, 이를 위해 실험 자료가 수집되고, 처리되어야 한다. 테스트 자료를 다양한 무차원 수로 분석함으로써 그 의존성이 확인될 수 있다. 그러한 무차원 수를 사용하여 명확한 기능적 특성이 나타나게 된다면, 그 무차원 수는 문제를 설명하기에 적합하다. |
| ○ 이 사건 제1항 발명의 기본 아이디어는 지멘스 반응기의 성능이 반응기 내의 유체 유동에 유의적으로 의존한다는 사실(구체적으로는 반응기 내의 큰 온도 차, 특히 가열된 봉 및 냉각된 벽의 온도 차에 기인한 자유대류와 기체 반응물의 공급에 기인한 강제대류가 유체 유동을 지배한다는 사실)을 발견한 것에 있다. |
| ○ 적절한 강제대류와 자유대류의 비, 즉 부력과 관성력의 비는 지멘스 반응기의 우수한 성능을 결정한다. |
○ 부력에 대한 식으로 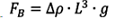 (식의 우변 각 변수는 순서대로 밀도차, 부력에 대한 특성 길이, 중력가속도임), 관성력에 대한 식으로
(식의 우변 각 변수는 순서대로 밀도차, 부력에 대한 특성 길이, 중력가속도임), 관성력에 대한 식으로 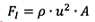 (식의 우변 각 변수는 밀도, 속도, 유동에 관련된 단면적임)을 사용할 수 있고, 부력 및 관성력의 무차원 비는 흔히 아르키메데스 수라고 불리는
(식의 우변 각 변수는 밀도, 속도, 유동에 관련된 단면적임)을 사용할 수 있고, 부력 및 관성력의 무차원 비는 흔히 아르키메데스 수라고 불리는 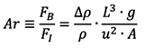 의 식인데, 이때 밀도 차 및 밀도의 비는 이상기체의 법칙을 사용하여
의 식인데, 이때 밀도 차 및 밀도의 비는 이상기체의 법칙을 사용하여 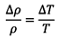 로 대체될 수 있으므로,
로 대체될 수 있으므로, 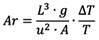 의 식이 도출된다.
의 식이 도출된다.
| ○ 공학 분야에서 주어진 문제에 대수적 항을 더 잘 적응시키기 위하여 무차원 수를 수정하는 것은 잘 알려진 것이고, 흔히 쓰이는 전략인바, 이 사건 제1항 발명에서 반응기 내의 자유대류에 관련된 온도는 가열된 봉의 온도인 Trod와 냉각된 벽의 온도인 Twall이므로, 양 온도의 차이를 관련된 온도 ΔT로 선택하는 것은 합리적이다(ΔT = Trod - Twall). |
○ 온도 T는 양 온도의 평균이 선택된다( 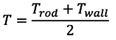 ).
).
| ○ 무차원 수에서 상수 인자들은 일반적으로 생략되므로 위 식의 ‘2’는 아르키메데스 수에서 무시될 수 있다. |
| ○ 가열된 봉의 길이를 자유대류에 대한 특성 길이 L로 사용하는 것은 명백하다. |
○ 지멘스 반응기에 관련된 속도 U는 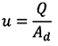 (Q는 실제 체적 유량, Ad는 노즐의 단면적의 총합으로서 아르키메데스 수의 A를 대체한다)로 대체될 수 있다.
(Q는 실제 체적 유량, Ad는 노즐의 단면적의 총합으로서 아르키메데스 수의 A를 대체한다)로 대체될 수 있다.
| ○ 앞선 식들을 종합하고, 차원 해석의 관점에서 무차원 수에 포함시키는 것이 타당한 필라멘트 봉의 수(n)를 포함시키면 다음의 식이 유도된다. |
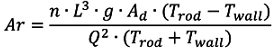
| ○ 위 식은 이 사건 아르키메데스 수와 기본적으로 동일한데, 단지 상수 인자 π 및 2가 생략되었을 뿐이다. |
| ○ 관성력 및 부력 모두 유체 점도에 의존하지 않으므로, 이 사건 아르키메데스 수 또한 유체 점도에 의존하지 않는다. |
| ○ 이 사건 아르키메데스 수를 유도하는 대안적인 방법으로, 다음과 같은 부록 1 기재의 식이 이용될 수 있다. |

| ○ 동적 점성도는 레이놀즈 수 뿐만 아니라 그라스호프 수에도 포함되는데, 이는 상기 무차원 수 모두가 점성력을 기술하고 있기 때문이고, 점성력은 아르키메데스 수에서 고려되지 않는다. 이 사건 아르키메데스 수는 자유 및 강제 대류로 인한 기체의 유동의 비를 기술하는 것이고, 압력 강하 또는 유사한 현상을 기술하지 않으므로, 이 사건 아르키메데스 수에 점도가 포함되지 않음은 명백하다. |
| ○ 필라멘트 봉의 수 및 노즐의 수력학적 지름을 포함하는 이 사건 아르키메데스 수는 반응기의 유동 조건을 고려하기 위하여 수정되었다. 수정된 결과는 무차원이고, 차원 해석의 관점에서 이는 가능하며, 정확한 것으로서, 이와 유사한 문제에 관한 몇 가지 과학 문헌들[훈(Huhn)의 2007년 박사학위 논문 ‘에너지 전환 체인에서의 수열 저장의 열역학적 해석 및 평가에 관한 기고’, 라바니, 마데싸 및 노르트의 2018년 논문 ‘아르키메데스 수 및 가열 속도가 환기되는 사무실의 열적 성층화에 미치는 영향에 관한 CFD 연구’, 다스칼라키의 1995년 저술, 아르지리우, 발라스 및 리코우디스의 2002년 저술]에 부합하는바, 이러한 예들은 필요한 경우 특별한 케이스들을 보다 정확하게 기술하기 위하여 무차원 수를 조정할 필요가 있다는 것을 나타내는데, 조정의 결과로서 얻어진 양의 그룹들이 여전히 무차원인 점 및 기술적인 시스템에 유의미한 영향을 갖는 물리적 양으로 조정이 이루어진다는 점이 중요하다. |
이에 따르면, 이 사건 아르키메데스 수는 이 사건 제1항 발명의 발명자들이 차원 해석의 관점에서 지멘스 반응기의 유동 조건을 고려하기 위하여 일반적으로 통용되는 아르키메데스 수를 수정함으로써 완성된 것이고, 그 수정의 방법으로, 많은 실험자료를 통해 지멘스 반응기에 유의미한 영향을 갖는 물리적 양을 선정한 후 이 사건 아르키메데스 수에 포함되도록 하는 방법 등이 사용되었다는 것인바, 그 각 진술의 논리 전개에 특히 부당한 점은 발견되지 아니한다.
또한 갑 제9, 10, 65, 66호증의 각 기재에 변론 전체의 취지를 종합하면, 아르키메데스 수의 산정과 관련하여 (i) 단일 개구를 가진 건물의 시스템에서, 그라스호프 수의 특성 길이를 개구의 높이로, 레이놀즈 수의 특성 길이를 방의 깊이로 각각 달리 선정한 후 이들을 통해 위 시스템 내 유체의 유동 조건에 대한 아르키메데스 수를 산정한 실험예, (ii) 환기구를 가진 가축 축사의 시스템에서, 위 시스템 내 유체의 유동 조건에 대한 아르키메데스 수를 산정하기 위하여 환기구의 수직 치수, 환기구의 수평치수 및 수력학적 지름에 의하여 수정된 아르키메데스 수를 도출한 실험예, (iii) 좌상단에 수평한 분출 유입구, 좌하단에 유체 배출구를 가지며, 우측 벽의 온도가 Tw로 유지되는 사각형 구멍(cavity)의 시스템에서, 레이놀즈 수 및 그라스호프 수의 특성 길이가 각각 배출구의 높이 및 구멍의 높이로 달리 선정되고, 레이놀즈 수의 특성 속도로 사용된 것은 유입구의 속도이며, 유입구의 온도와 구멍 내의 가열된 벽면의 온도가 달라 동적 점성도가 상이함에도 불구하고 레이놀즈 수와 그라스호프 수의 동적 점성도가 동일하다고 보아 위 시스템 내 유체의 유동 조건에 대한 아르키메데스 수의 분자 및 분모에서 위 각 동적 점성도를 소거함으로써 위 아르키메데스 수에서 동적 점성도를 고려하지 않은 실험예, (iv) 환기를 위하여 2개의 유입구 및 1개의 유출구를 가짐과 동시에, 내부에 열원으로서의 사람이 있는 사무실의 시스템에서, 유입구 및 사무실 내부의 상이한 온도로 인하여 자유대류(그라스호프 수에 대응)에 관한 동적 점성도와 강제대류(레이놀즈 수에 대응)에 관한 동적 점성도가 서로 상이함에도 불구하고 위 시스템 내 유체의 유동 조건에 대한 아르키메데스 수의 분자 및 분모에서 위 각 동적 점성도를 소거함으로써 위 아르키메데스 수에서 동적 점성도를 고려하지 않은 실험예 등이 기재된 각 논문이 존재하는 사실을 인정할 수 있다.
(나) 위 인정 사실을 종합하여 보면, 시스템 내부의 유체 유동에 대한 아르키메데스 수를 산정함에 있어, 각 시스템의 특성에 따라 다양한 물리적 양들이 변수로 선정되고, 각 물리적 양이 상호 정확하게 일치함이 담보되지 않음에도 불구하고 서로 약분되는 경우가 있으며, 상수가 무시되는 등의 다양한 아르키메데스 수의 형태가 존재함을 인정할 수 있는바, 이에 비추어 이 사건 아르키메데스 수에서 서로 다른 특성 길이가 적용되었고, 정확히 일치하지 않는 물리적 양이 약분되었으며, 부력에 관한 일반적인 예와 다른 ΔT가 산정되었고, 상수 부분이 상이한 형태의 이 사건 아르키메데스 수가 유도되었다는 등의 사정이 기술 상식에 반하는 과학적·기술적 오류에 해당한다고 볼 수 없고, 을 제1 내지 4, 17호증(각 가지번호 포함, 이하 같다)의 각 기재만으로는 위 인정을 뒤집기에 부족하며, 달리 반증이 없다.
(다) 결국 피고의 위 주장은 이유 없고, 이 사건 아르키메데스 수에 관한 기술 오류는 인정되지 아니한다.
라) 이 사건 제1항 발명의 효과가 이 사건 명세서에서 구체적인 실험, 실시예 등으로 증명되었는지 여부
(1) ① 이 사건 명세서에는, 이 사건 제1항 발명의 작용·효과에 대하여 ‘본 발명의 목적은 전술한 문제를 해소하기 위한 것이다(식별번호 [0052])’라고 기재되어 있는바, 이 사건 명세서의 배경기술에서 종래 실리콘 봉의 제조방법에 관한 단점으로 설명된 제반 문제점들, 즉 봉의 표면 특성 불량 등 생성물의 품질 문제; 비에너지가 낮고, 봉이 반응기 안에서 넘어지며, 실리콘 분진이 형성되고, 과열이 일어나며, 실리콘 봉이 용융되는 등의 제조 공정 경제성 악화; 봉의 전장에 걸쳐 일정한 구조 또는 형태를 달성하는 것과 동시에 충분히 높은 증착 속도를 달성하는 것이 불가능한 문제; 봉 및 브릿지의 누출 방지와 동시에 높은 증착 속도와 개선된 에너지 효율을 얻는 것이 불가능한 문제; 봉 직경의 불일정성 문제; 분진 증착(식별번호 [0016] 내지 [0051] 참조) 등이 이 사건 제1항 발명을 통해 해결될 수 있음이 제시된 것으로 보인다. 또한 반응기의 크기, 반응기 내 필라멘트 봉의 수 및 길이와 관계없이 이 사건 제1항 발명의 제조방법이 적용될 수 있는 점, 이 사건 제1항 발명의 제조방법에 의할 경우 봉의 길이에 걸쳐 직경의 편차가 작고, 실리콘 봉의 형태가 반응기 내 위치에 관계없이 모두 유리한 형태를 가지게 되는 점(식별번호 [0058] 내지 [0089] 참조)도 기재되어 있다.
② 또한 이 사건 명세서에는 종래 공지되어 있던 다결정 실리콘의 제조방법에 따른 비교실시예가 기재되어 있다.
구체적으로, 종래 공지되어 있던 다결정 실리콘의 제조방법에 따른 비교실시예로서, 이 사건 명세서에는 도 1의 포인트 41 내지 46, 포인트 7에 해당하는 2개 공정의 각 공정변수들 및 이에 대응하는 실험 결과가 기재되어 있는바, 위 실험 결과에 대한 기재 내용으로는 ‘EP 2 067 744 A2 주21) 에 개시된 공정에 대한 아르키메데스 수의 그래프는 본 발명의 아르키메데스 수의 범위에 못 미치며 전혀 다른 특성을 보여주고 있(다)(식별번호 [0111])’, ‘특히, 넘어지는 봉의 비율이 증가되는 것으로 관찰된다. 증착 속도 역시 균일한 떨어지는 형태가 허용되는 때에만 충분히 높다. 아르키메데스 수의 증가가 이러한 문제들을 제거할 수 있다는 사실이 놀랍다(식별번호 [0112])’, ‘DE 29 661 A1 주22) 에 개시된 공정은 또한 충전 수준의 함수로서 아르키메데스 수의 그래프를 보여주고 있는데, 이것은 본 발명의 범위보다 낮다(EP 2 067 744 A2에 개시된 공정과 유사하지만, 구체적인 그래프는 없다)(식별번호 [0113])’, ‘봉의 구조의 균일성과 관련하여 DE 29 12 661 A1에 기재된 장점이 이러한 공정에서 관찰될 수 있지만, 이 공정은 다른 단점들을 상당히 나타낸다(식별번호 [0116])’, ‘예를 들어, 아르키메데스 수와 관련하여 본 발명의 범위 내에 있는 공정들 보다 비에너지 소비가 훨씬 높다’(식별번호 [0117])’, ‘반면, 본 발명의 공정의 경우 비에너지 소비가 10-20% 낮다(식별번호 [0118])’, ‘또한, 비교 실시예의 공정에 따르면, 넘어지는 봉의 비율이 뚜렷하게 증가한다(식별번호 [0119])’는 내용이 개시되어 있다.
③ 한편, 이 사건 명세서에는 위 비교실시예들에 대비되는 이 사건 제1항 발명에 따른 실시예가 기재되어 있는바, 구체적으로는 도 1의 포인트 11 내지 13, 포인트 21 내지 23, 포인트 31 내지 34에 해당하는 3개 공정의 각 공정변수들이 표 3 내지 5에 공정별로 기재되어 있다. 이에 대응하는 실험 결과로는 위 3개 공정을 통틀어 ‘서로 다른 반응기가 사용되었는데, 이들 반응기는 반응기의 체적 및 봉의 수에 있어서 서로 상이하다(식별번호 [0123])’는 내용만이 개시되어 있다.
④ 위와 같은 이 사건 명세서상 기재 내용을 종합하면, 이 사건 명세서에는 이 사건 제1항 발명에 대한 구체적 실험예로서 3개 공정(1개 공정당 3 내지 4개 포인트에 해당하는 각 공정변수들 세트 포함)이, 종래 공지기술에 대한 구체적 실험예로서 2개 공정(EP 2 067 744 A2의 경우 6개 포인트에 해당하는 공정변수들 세트가 포함되어 있고, DE 29 12 661 A1의 경우 1개 포인트에 해당하는 공정변수들 세트가 포함되어 있음)이 각 개시되어 있음을 알 수 있다.
(2) 결국 이 사건 명세서상 구체적인 실험, 실시예 등으로부터 증명되는 이 사건 제1항 발명의 구성에 따른 효과는 위 3개 공정(1개 공정당 3 내지 4개 포인트에 해당하는 각 공정변수들 세트 포함)에 대한 효과에 불과하다 할 것인바, 이는 이 사건 제1항 발명의 구성 전체에 의한 효과가 이 사건 명세서에서 구체적인 실험, 실시예 등으로 증명된 것이라고 볼 수 없다. 그러나 반드시 구체적인 실시예가 기재되어 있지 않다고 하더라도 통상의 기술자가 명세서 기재 내용에 출원 시 기술 수준을 더하여 발명의 구성에 따른 효과를 능히 예측하여 발명의 구성 및 효과를 정확하게 이해하고 재현하는 것이 용이한 경우도 있으므로, 이 사건 제1항 발명이 그에 해당하는지 여부를 아래 항에서 살펴본다.
마) 이 사건 제1항 발명의 효과가 통상의 기술자의 출원 시 기술 수준으로 능히 예측될 수 있는지 여부
(1) 이 사건 제1항 발명이 지멘스 반응기 내에서 화학 반응을 통해 다결정 실리콘을 제조하는 방법에 관한 화학발명이면서, 이 사건 명세서 기재를 통해 새롭게 정의된 충전 수준과 이 사건 아르키메데스 수 사이의 상관관계를 연산식과 수치로 한정한 파라미터발명에 해당함은 앞서 본 바와 같다.
(2) 따라서 화학발명의 특성상 실험데이터가 제시된 실험예가 기재되어 있지 않으면 이 사건 명세서에 기재된 개괄적 효과에 불구하고 통상의 기술자가 이 사건 제1항 발명의 효과를 명확하게 이해하고 용이하게 재현할 수 있다고 보기 어려운 구성 부분이 다수 존재할 수 있고, 나아가 새로운 파라미터가 제시된 파라미터발명의 특성상 그 기술적 의의 또는 작동원리(파라미터의 유도과정 등)가 명세서상 개시되지 않을 경우 이 사건 명세서상 개괄적 효과 기재에 불구하고 이 사건 제1항 발명의 구성 전체에 대한 효과의 예측가능성 내지 실현가능성이 현저히 부족하게 되는 경우가 발생할 수 있다.
(3) 한편, 이 사건 제1항 발명에서 수치범위로 한정한 공정 대상이 ‘5%까지의 충전 수준 FL에 대해서는 함수 Ar = 2000 x 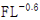 에 의한 하한값과 함수 Ar = 17000 x
에 의한 하한값과 함수 Ar = 17000 x 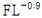 에 의한 상한값으로 정해지는 범위 내이고, 충전 수준 FL이 5% 보다 큰 경우에는 750 내지 4000의 범위 내인 모든 공정’인바, 그 대상이 되는 수치범위가 매우 광범위한 것으로 보이고, 이 사건 아르키메데스 수와 FL의 함수관계를 구성하는 연산식에 포함된 공정변수가 총 7개인 점을 감안하면, 위 수치범위 중 어느 특정한 하나의 값에 해당하는 이 사건 아르키메데스 수일지라도 이에 해당되는 공정변수들 세트에는 훨씬 많은 수의 조합들이 포함되어 있을 것으로 예상된다.
에 의한 상한값으로 정해지는 범위 내이고, 충전 수준 FL이 5% 보다 큰 경우에는 750 내지 4000의 범위 내인 모든 공정’인바, 그 대상이 되는 수치범위가 매우 광범위한 것으로 보이고, 이 사건 아르키메데스 수와 FL의 함수관계를 구성하는 연산식에 포함된 공정변수가 총 7개인 점을 감안하면, 위 수치범위 중 어느 특정한 하나의 값에 해당하는 이 사건 아르키메데스 수일지라도 이에 해당되는 공정변수들 세트에는 훨씬 많은 수의 조합들이 포함되어 있을 것으로 예상된다.
(4) 또한 앞서 본 이 사건 명세서의 기재 내용을 종합하여 보면, (i) 이 사건 명세서에 개시된 구체적 실험, 실시예는 종래 기술에 따른 2개 공정(총 7개의 공정변수들 세트), 이 사건 제1항 발명에 따른 3개 공정(총 10개의 공정변수들 세트)에 불과한 점, (ii) 그 기재된 효과 역시 종래 기술의 실험 결과 부분에 ‘넘어지는 봉의 비율이 증가’, ‘증착 속도 역시 균일한 떨어지는 형태가 허용되는 때에만 충분히 높다. 아르키메데스 수의 증가가 이러한 문제들을 제거할 수 있다는 사실이 놀랍다’, ‘이 공정은 다른 단점들을 상당히 나타낸다’, ‘비에너지 소비가 훨씬 높다’, ‘반면, 본 발명의 공정의 경우 비에너지 소비가 10-20% 낮다’, ‘비교 실시예의 공정에 따르면, 넘어지는 봉의 비율이 뚜렷하게 증가한다’는 등의 정성적 또는 간략한 정량적 기재만이 나타나 있고, 이 사건 제1항 발명의 실시예에 따른 실험 결과로는 ‘서로 다른 반응기가 사용되었는데, 이들 반응기는 반응기의 체적 및 봉의 수에 있어서 서로 상이하다’는 내용만이 나타나 있는 점, (iii) 이 사건 제1항 발명의 유일한 구체적 실시예로서 개시된 위 3개 공정에 대한 이 사건 아르키메데스 수의 경우, 이 사건 제1항 발명의 수치범위, 즉 충전 수준의 함수인 이 사건 아르키메데스 수의 상한값과 하한값을 구성하는 각 수치범위의 한계선들에 근접한 수치를 나타내고 있지 아니하고, 위 3개 공정의 각 수치가 서로 유사하거나 일정한 패턴을 가진다고도 보기 어려운 점(이 사건 명세서 도 1 참조), (iv) 이 사건 제1항 발명의 구체적 실시예인 3개 공정에서 각 측정된 반응 중의 실리콘 봉의 온도(Trod)가 반응 진행에 따라 상이한 온도를 나타낸 것에 반하여(이 사건 명세서 표 3 내지 5 참조), 공지기술인 비교실시예에 해당하는 2개 공정의 경우 측정된 반응 중의 실리콘 봉의 온도(Trod)가 모두 ‘393K’의 단일한 온도로 나타나 있어(이 사건 명세서 표 1, 2 참조) 공지기술인 위 2개 공정에 대한 비교실험이 실제 이루어진 것인지에 대한 의문이 제기될 수 있는 상황인 점 등을 인정할 수 있다.
(5) 나아가 갑 제6호증의 1 내지 3의 각 기재에 변론 전체의 취지를 종합하면, 이 사건 특허발명의 기본 아이디어가 ‘지멘스 반응기의 성능이 반응기 내의 유체 유동에 유의적으로 의존한다는 사실을 발견한 것’임을 인정할 수 있고, 이 사건 명세서에도 ‘다결정 실리콘의 증착을 위한 지멘스 반응기에 대해서는 아르키메데스 수와 관련하여 아직 아무런 평가가 이루어져 있지 않다(식별번호 [0062])’고 기재되어 있으며, 원고가 이 사건 소송에서, 지멘스 공정 내 이 사건 아르키메데스 수와 FL의 상관관계에 대한 이 사건 제1항 발명이 차원 해석 및 수많은 실험을 통해 완성된 것임을 강조하여 온 사정을 종합하여 보면, 지멘스 반응기 내 유체 유동에 관한 이 사건 제1항 발명의 출원 시의 기술 수준은 별다른 지식이 없는 미미한 수준에 불과하였던 것으로 보인다.
(6) 위와 같은 이 사건 제1항 발명의 특성, 청구된 수치범위의 폭이 넓은 점, 이 사건 명세서 기재 내용의 구체적인 정도 등에 비추어 볼 때, 통상의 기술자가 이 사건 명세서의 기재 내용에 출원 시의 기술 수준을 더하여 보더라도 이 사건 명세서에 구체적 실시예로서 기재된 위 3개 공정 및 그로 인한 효과에 더하여 이에 인접한 이 사건 제1항 발명 중 매우 한정된 수치범위의 구성 및 그로 인한 효과만을 예측할 수 있을 뿐, 그 나머지 범위의 구성 및 그로 인한 효과에 대하여는 통상의 기술자가 과도한 실험이나 특수한 지식을 부가하지 아니하고서는 이를 예측하거나 재현할 수 있는 가능성이 현저히 부족하다고 할 것이다.
(7) 결국 이 사건 제1항 발명의 효과는 통상의 기술자의 출원 시 기술 수준을 더하여 보더라도 그 구성의 전체 수치범위에 대하여는 이를 능히 예측할 수 없다고 봄이 타당하다.
바) 소결
이 사건 제1항 발명의 효과는 이 사건 명세서에 그 청구된 수치범위 전체에 걸쳐 통상의 기술자가 충분히 예측할 수 있을 정도로 기재되어 있다고 볼 수 없다.
3) 종합
가) 이 사건 제1항 발명에 대한 이 사건 명세서상 발명의 상세한 설명은 통상의 기술자가 그 발명을 쉽게 실시할 수 있도록 명확하고 상세하게 기재되었다고 볼 수 없다.
나) 나아가 이 사건 제2 내지 8항 발명은 독립항인 이 사건 제1항 발명의 종속항들로서, 이 사건 제1항 발명의 내용이 위 각 종속항에 모두 인용되어 있다 할 것인바, 위와 같이 이 사건 제1항 발명의 구성 및 효과에 대한 발명의 상세한 설명 기재불비가 인정되는 이상 이 사건 제2 내지 8항 발명 역시 통상의 기술자가 그 발명을 쉽게 실시할 수 있도록 명확하고 상세하게 기재되었다고 볼 수 없다.
다) 따라서 이 사건 특허발명 모두 발명의 상세한 설명에 통상의 기술자가 그 발명을 쉽게 실시할 수 있도록 명확하게 상세하게 기재되었다고 볼 수 없다.
4. 이 사건 특허발명의 ‘청구범위’ 기재불비에 대한 판단
가. 관련 규정 및 판단 기준
구 특허법 제42조 제4항 제2호 는 청구범위에는 발명이 명확하고 간결하게 기재될 것을 규정하고 있고, 특허발명의 보호범위는 청구범위에 적혀 있는 사항에 의하여 정하여지므로, 청구범위에는 명확한 기재만이 허용되고, 발명의 구성을 불명료하게 표현하는 용어는 원칙적으로 허용되지 않는다( 대법원 2006. 11. 24. 선고 2003후2072 판결 , 2014. 7. 24. 선고 2012후1613 판결 등 참조). 여기서 발명이 명확하게 적혀 있는지 여부는, 통상의 기술자가 발명의 상세한 설명이나 도면 등의 기재와 출원 당시의 기술 상식을 고려하여 청구범위에 기재된 사항으로부터 특허를 받고자 하는 발명을 명확하게 파악할 수 있는지에 따라 개별적으로 판단하여야 하고, 단순히 청구범위에 사용된 용어만을 기준으로 하여 일률적으로 판단하여서는 안 된다. 또한 청구범위의 기재 내용이 관점에 따라 다양한 방식으로 해석될 수 있는 경우에는 청구범위로서 요구되는 명확성과 간결성 요건을 충족하지 못하였다고 보아야 한다( 대법원 2017. 4. 7. 선고 2014후1563 판결 참조).
나. 판단
1) 이 사건 제1항 발명은, 봉의 부피(Vrods), 벽의 온도(Twall), 체적 유량(Q) 등의 공정변수들을 포함하는 이 사건 아르키메데스 수 및 FL 등으로 구성되어 있으나, 앞서 이 사건 제1항 발명의 상세한 설명 기재불비 여부에서 살펴본 바와 같이 봉의 부피(Vrods), 벽의 온도(Twall), 체적 유량(Q)의 각 측정 방법이 명확하지 아니하므로, 이 사건 제1항 발명은 청구범위에 발명이 명확하게 기재되어 있다고 할 수 없다.
2) 또한 이 사건 제2 내지 8항 발명은 독립항인 이 사건 제1항 발명의 종속항들로서, 이 사건 제1항 발명의 내용이 위 각 종속항에 모두 인용되어 있다 할 것인바, 위와 같이 이 사건 제1항 발명에 포함된 공정변수들인 봉의 부피(Vrods), 벽의 온도(Twall), 체적 유량(Q)의 각 측정 방법이 명확하지 아니한 이상 위 공정변수들을 포함하는 이 사건 제2 내지 8항 발명 역시 청구범위에 발명이 명확하게 기재되어 있다고 할 수 없다.
5. 결론
따라서 이 사건 특허발명은 발명의 상세한 설명 및 청구범위에 기재불비가 있다 하라 것인바, 신규성 및 진보성 판단으로 더 나아가 살필 필요 없이 그 등록이 무효로 되어야 하므로, 이와 결론을 같이 한 이 사건 심결은 적법하다. 그렇다면 이 사건 심결의 취소를 구하는 원고의 청구는 이유 없으므로, 이를 기각하기로 하여 주문과 같이 판결한다.
주1) 이 사건 심결에서 ‘비교대상발명 1 내지 4’로 하여 인용된 발명들(각 선행발명 1 내지 4에 대응함)로서, 후술하는 이 사건 판단에서 다루어지지 아니하는바, 각 발명의 구체적인 내용은 생략한다.
주2) 이 사건 심결에서는 발명의 상세한 설명 부분 관련 기재불비에 대한 근거 법률로 ‘구 특허법(2011. 5. 24. 법률 제10716호로 개정되기 전의 것)’을, 특허청구범위 부분 관련 기재불비에 대한 근거 법률로 ‘구 특허법(2014. 6. 11. 법률 제12753호로 개정되기 전의 것)’을 각 적시하였으나, 이 사건 특허발명의 출원일은 ‘2011. 8. 25.’로서, 발명의 상세한 설명 부분 관련 기재불비에 대한 근거 법률은 ‘구 특허법(2013. 3. 23. 법률 제11690호로 개정되기 전의 것)’이 적용되어야 하고(해당 부칙에 의해 시행일인 2011. 7. 1. 이후 최초로 출원하는 특허출원부터 적용함), 특허청구범위 부분 관련 기재불비에 대한 근거 법률의 해당 조문 내용은 이 사건 특허발명의 출원일 당시부터 2014. 6. 11.자 특허법 일부 개정이 이루어지기 이전까지 동일하므로, 이 사건 판결에서는 기재의 편의상 발명의 상세한 설명 및 특허청구범위에 관한 기재불비 근거 법률을 모두 ‘구 특허법(2013. 3. 23. 법률 제11690호로 개정되기 전의 것)’으로 기재하고, 위와 같은 취지에서 이 사건 심결에서 적시한 ‘구 특허법(2011. 5. 24. 법률 제10716호로 개정되기 전의 것) 제42조 제3항’을 이에 대응하는 ‘구 특허법(2013. 3. 23. 법률 제11690호로 개정되기 전의 것) 제42조 제3항 제1호‘로 바꾸어 판단하기로 하되, 해당 각 조문의 변경 전후 내용은 실질적으로 동일하다.
주3) 이 사건 특허발명 중 독립항으로서 범위가 가장 넓은 이 사건 제1항 발명에 대하여 먼저 보기로 한다.
주4) 이 사건 제1항 발명의 내용과 동일하다.
주5) 이 사건 명세서에서 ‘다결정 실리콘’과 동일한 의미로 혼용되고 있다.
주6) ‘실리콘 봉’과 동일한 의미이다.
주7) ‘실리콘 봉’과 동일한 의미이다.
주8) 원고가 이 사건 소송에 이르러 이 사건 제1항 발명의 효과 증명을 위해 제출한 자료들(갑 제47, 58, 82, 83호증)은 이 사건 제1항 발명의 출원 당시 제출된 것이 아닐 뿐만 아니라, 이 사건 아르키메데스 수나 충전수준을 구성하는 개별 공정변수 세트들의 실제 수치들을 포함하고 있지도 아니하다.
주9) U= 1/(dw/k + I/ho)
주10) 갑 제86호증(Incropera et al Fundamentals of Heat and Mass Transfer 7th ed John Wiley Sons pp 447-448)
주11) 갑 제87호증(Garvin Understand the thermal design of jacketed vessels Chemical Engineering Progress, June 1999, pp 4, 5)
주12) 원고는 해당 Nu 수들이 ‘지멘스 반응기와 같이 반응기 내벽 바깥에 냉매가 흐르는 쟈켓이 장착된 반응기에서 열전달 계수를 구하는 Nu 수’ 또는 ‘반응기의 내벽 주위에 1/2 원 또는 1/3 원 모양의 단면을 갖는 코일을 장착한 쟈켓이 장착된 반응기에서 열전달 계수를 구하는 Nu 수’라고 주장하였다(원고의 2019. 12. 4.자 준비서면 10, 11쪽 참조).
주13) 위 11)항 기재 부분 참조
주14) 원고의 2019. 6. 24.자 준비서면 22, 23쪽, 2019. 10. 18.자 준비서면 37, 38쪽 참조
주15) 이 사건 아르키메데스 수가 아닌, 종래 공지되어 있었던 아르키메데스 수를 의미하는 것으로 보인다.
주16) 원고의 2019. 6. 21.자 준비서면 7쪽 첫 번째 단락 참조
주17) 위 ‘2. 나. 1)항’ 기재 피고 주장의 요지 부분에 해당하는 내용이다(판결서 22쪽 참조). 위 주장 부분에는 ‘유도과정’ 및 ‘기술 오류’에 관한 부분 외에 ‘이 사건 아르키메데스 수와 발명 효과 사이의 관계’에 관한 부분도 포함되어 있으나, 위 ‘효과와의 관계’ 부분은 직전 항에서 밝힌 ‘① 발명 효과의 구체적 실험, 실시예 등에 의한 증명, ② 통상의 기술자의 예측가능성 여부’에 포함되어 함께 판단될 것인바, 별도로 판단하지 않는다.
주18) 피고의 2019. 8. 21.자 준비서면 8쪽 참조
주19) 피고의 2019. 6. 21.자 요약쟁점정리서면 1쪽 등에서 동일한 용어로 사용된 것으로 보인다.
주20) 피고가 이 사건 아르키메데스 수의 유도과정에 과학적 오류가 있다고 주장하였고, 그 유도과정이 밝혀질 필요가 없음은 앞서 본 바와 같으나, 피고의 위 주장은 이 사건 아르키메데스 수 자체에 과학적 오류가 있어 발명의 용이한 실시가 불가능하다는 취지로 선해할 수 있다.
주21) 종래 공지되어 있던 다결정 실리콘의 제조방법에 해당한다.
주22) 또 다른 종래 공지의 다결정 실리콘의 제조방법에 해당한다.
관련문헌
- 이지영 파라미터발명과 명세서의 실시가능 요건 : -판단기준 및 고려 요소들을 중심으로- LAW & TECHNOLOGY 제17권 제6호 / 서울대학교 기술과법센터 2021
본문참조판례
특허심판원이 2018. 10. 10. 2017당2655 사건에 관하여 한 심결
2017당2655호
서울중앙지방법원 2017가합509596
대법원 2011. 10. 13. 선고 2010후2582 판결
대법원 2001. 11. 30. 선고 2000후2958, 2001후65 판결
대법원 2015. 9. 24. 선고 2013후525 판결
대법원 2010. 2. 25. 선고 2007다85980 판결
대법원 2006. 11. 24. 선고 2003후2072 판결
2014. 7. 24. 선고 2012후1613 판결
대법원 2017. 4. 7. 선고 2014후1563 판결
본문참조조문